Solveeit Logo
Login

Question

Question: The value of $(\cos\alpha + \cos\beta)^2 + (\sin\alpha + \sin\beta)^2$ is...

The value of (cos⁡α+cos⁡β)2+(sin⁡α+sin⁡β)2(\cos\alpha + \cos\beta)^2 + (\sin\alpha + \sin\beta)^2 is

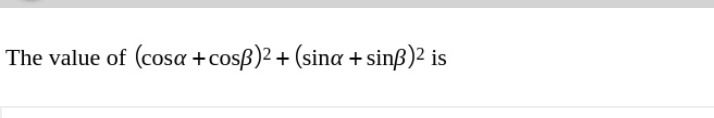
Answer

2 + 2cos(α-β)

Explanation

Solution

We simplify by expanding the squares:

(cos⁡α+cos⁡β)2=cos⁡2α+2cos⁡αcos⁡β+cos⁡2β(\cos\alpha + \cos\beta)^2 = \cos^2\alpha + 2\cos\alpha\cos\beta + \cos^2\beta (sin⁡α+sin⁡β)2=sin⁡2α+2sin⁡αsin⁡β+sin⁡2β(\sin\alpha + \sin\beta)^2 = \sin^2\alpha + 2\sin\alpha\sin\beta + \sin^2\beta

Adding,

cos⁡2α+sin⁡2α+cos⁡2β+sin⁡2β+2(cos⁡αcos⁡β+sin⁡αsin⁡β)\cos^2\alpha + \sin^2\alpha + \cos^2\beta + \sin^2\beta + 2(\cos\alpha\cos\beta + \sin\alpha\sin\beta)

Since cos⁡2θ+sin⁡2θ=1\cos^2\theta+\sin^2\theta=1 for any angle,

=1+1+2(cos⁡αcos⁡β+sin⁡αsin⁡β)=2+2cos⁡(α−β)= 1 + 1 + 2(\cos\alpha\cos\beta+\sin\alpha\sin\beta) = 2 + 2\cos(\alpha-\beta)

Thus, the value is:

2+2cos⁡(α−β)2 + 2\cos(\alpha-\beta)

Expand both squares, use the Pythagorean identity, and recognize the cosine addition formula.