Question
Question: The value of $\cos \left( 2\sin^{-1}\left(\frac{-1}{6}\right) \right) + \tan \left( \sec^{-1}\left(...
The value of
cos(2sin−1(6−1))+tan(sec−1(12−13)) is
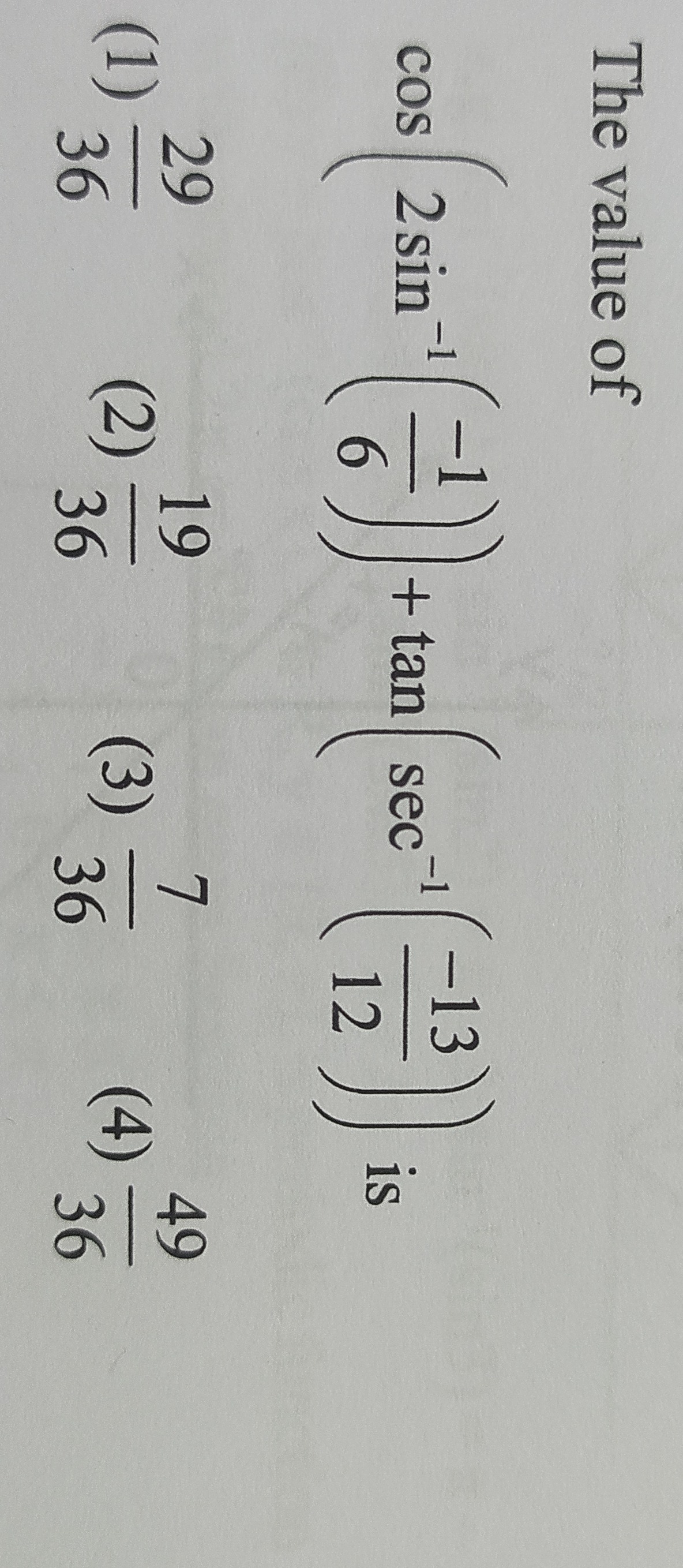
3629
3619
367
3649
3619
Solution
Let's evaluate the two terms separately.
Term 1: cos(2sin−1(6−1))
Let θ=sin−1(6−1). Then sin(θ)=−61.
We need to find cos(2θ). Using the double angle identity cos(2θ)=1−2sin2(θ), we have:
cos(2θ)=1−2(−61)2=1−2(361)=1−181=1818−1=1817.
Term 2: tan(sec−1(12−13))
Let ϕ=sec−1(12−13). Then sec(ϕ)=−1213.
We need to find tan(ϕ). Using the identity tan2(ϕ)+1=sec2(ϕ), we have:
tan2(ϕ)=sec2(ϕ)−1=(−1213)2−1=144169−1=144169−144=14425.
So, tan(ϕ)=±14425=±125. Since sec(ϕ) is negative, ϕ is in the second quadrant, so tan(ϕ) is negative.
Thus, tan(ϕ)=−125.
Now, we add the values of the two terms:
Value = 1817+(−125)=1817−125=3634−3615=3619.
Therefore, the value of the expression is 3619.
