Question

The value of $c$ in the Lagrange’s mean value theorem for $f\left( x \right) = \log x$ on $\left[ {1,e} \right]$
A. $\dfrac{e}{2}$
B. $e - 1$
C. $e - 2$
D. $1 - e$

Answer 1

Begin by finding the value of $f'\left( x \right)$ and then substituting $x = c$. We will then find the value of $f'\left( c \right)$ from Lagrange’s mean value theorem. Then, we will compare the values of $f'\left( c \right)$ from both the equations to find the value of $c$.

Complete step by step solution:
We know that the Lagrange’s mean value theorem states that, if a function $f\left( x \right)$ is continuous in the interval $\left[ {a,b} \right]$ and is differentiable in $\left( {a,b} \right)$, then there will be at least one point $c$ in the interval $\left[ {a,b} \right]$ such that
$f'\left( c \right) = \dfrac{{f\left( b \right) - f\left( a \right)}}{{b - a}}$
Here, we have $f\left( x \right) = \log x$ and $\left[ {a,b} \right]$=$\left[ {1,e} \right]$
We will draw the graph of the function $f\left( x \right) = \log x$ and check if the function is continuous on $\left[ {1,e} \right]$.

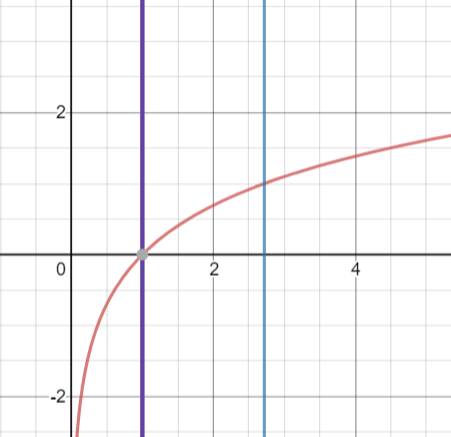
From the graph we can see that the function is continuous on $\left[ {1,e} \right]$.
Now, let us take the derivative of the given function $f\left( x \right) = \log x$
$f'\left( x \right) = \dfrac{1}{x}$
$f'\left( x \right)$ exists for all values of $x$ in the given interval. Therefore, the given function is differentiable on $\left[ {1,e} \right]$
Hence,
$f'\left( c \right) = \dfrac{1}{c}$ eqn. (1)
Then, by applying Lagrange’s mean value theorem on $\left[ {1,e} \right]$.
$f'\left( c \right) = \dfrac{{f\left( b \right) - f\left( a \right)}}{{b - a}} = \dfrac{{f\left( e \right) - f\left( 1 \right)}}{{e - 1}} = \dfrac{{\log e - \log 1}}{{e - 1}}$
Since, ${\log _e}\left( 0 \right) = 0$ and ${\log _e}\left( e \right) = 1$, therefore,
$f'\left( c \right) = \dfrac{{1 - 0}}{{e - 1}} = \dfrac{1}{{e - 1}}$ eqn. (2)
On equating equations (1) and (2), we will get,
$\dfrac{1}{c} = \dfrac{1}{{e - 1}} \\\ \Rightarrow c = e - 1 \\\$
Hence, option B is correct.

Note:
We can apply Lagrange’s mean value theorem only when the function is continuous and differentiable in the given interval. Also, one must know how to draw a graph of the functions and how to calculate derivatives to avoid mistakes in these types of questions.