Question

The value of c for which the set \left\\{ \left( x,y \right)\left| {{x}^{2}}+{{y}^{2}}+2x\le 1 \right| \right\\}\cap \left\\{ \left( x,y \right)\left| x-y+c\ge 0 \right| \right\\} contains only one point in common is?
A.$\left( -\infty ,-1 \right)\cup \left( 3,\infty \right)$
B.\left\\{ -1,3 \right\\}
C.\left\\{ -3 \right\\}
D.\left\\{ -1 \right\\}

Answer 1

Hint: To solve this question, we will first determine the curves which are formed from the equation ${{x}^{2}}+{{y}^{2}}+2x=1$ and $x-y+c=0$ . After finding the curve, we will plot the region ${{x}^{2}}+{{y}^{2}}+2x\le 1$ and then we will find that value(s) of c at which the region $x-y+c=0$ touches the region ${{x}^{2}}+{{y}^{2}}+2x\le 1$ at only one point.

Complete step-by-step answer:
In this question, we are given that when the set \left\\{ \left( x,y \right)\left| {{x}^{2}}+{{y}^{2}}+2x\le 1 \right| \right\\} is intersected with the set \left\\{ \left( x,y \right)\left| x-y+c\ge 0 \right| \right\\}, then we will get only one intersection point. The equations given in sets are basically regions’ and plot them on the graph. To find the regions, we will first set, we have:
${{x}^{2}}+{{y}^{2}}+2x=1$ ………………………… (1)
The general equation of a circle is ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ . So, equation (1) is an equation of a circle. So we will obtain a circular region in the graph. The circle having equation ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c'=0$ has centre $\left( -g,-f \right)$ and radius $\sqrt{{{g}^{2}}+{{f}^{2}}-c'}$ . Now we will compare the general equation of the circle with the circle in the equation.
Thus, we have:
$\begin{aligned} & 2gx=2x \\\ & \Rightarrow 2g=2 \\\ \end{aligned}$
$\Rightarrow g=1$ ……………………. (2)
$2fy=0$
$\Rightarrow f=0$ …………………….. (3)
$c'=-1$ ………………………... (4)
Therefore, the centre of the circle in equation is $\left( -1,0 \right)$ and its radius $=\sqrt{{{\left( 1 \right)}^{2}}+{{0}^{2}}-\left( -1 \right)}=\sqrt{1+1}=\sqrt{2}$ . Now, we will plot this circular region in a graph.
As ${{x}^{2}}+{{y}^{2}}+2x\le 1$ satisfies when we put the origin $\left( 0,0 \right)$ in it, so, the region will be inner circular region. So, we have:

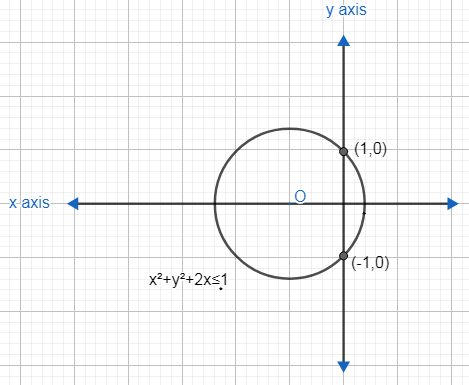
Now, we will convert the in equation given in second set to equation:
$x-y+c=0$
$\Rightarrow y=x+c$ …………………………… (5)
The above equation is an equation of a straight line with slope =1 and intercept =c. Now, we will determine the region in this set. It is given that $x-y+c\ge 0$ . When, we put origin $\left( 0,0 \right)$ in equation, we get:
$\begin{aligned} & 0-0+c\ge 0 \\\ & \Rightarrow c\ge 0 \\\ \end{aligned}$
Now, we do not do anything about c so. We will form two cases.
Case: 1 $c\ge 0$ .
If $c\ge 0$ then the region of the graph will be towards the origin as shown:

Case: 2 $c<0$
If $c<0$then the region of the graph will be away from the origin as shown:

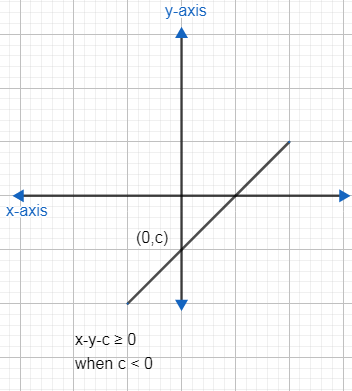
Now, we will merge the graphs so that they are only common. Clearly, we can see that when the graph in the first set and graph of the second set's first case are plotted, the number of solutions would always be infinite because they will have infinite points common in them. But we want that only one point should be common. Hence case 1 is not possible. Now, we will check the same for case 2. Now, we want that there should be only one solution. It would be possible only when the line $x-y-c=0$ touched the circle ${{x}^{2}}+{{y}^{2}}+2x-1=0$ at only one point. This is possible only when the line is tangent to the circle. This is as shown:

Now, we will find the general equation of tangent of the circle ${{x}^{2}}+{{y}^{2}}+2x-1=0$. Thus, we have:
$\begin{aligned} & {{y}^{2}}=1-{{x}^{2}}-2x \\\ & \Rightarrow y=\pm \sqrt{1-{{x}^{2}}-2x} \\\ \end{aligned}$
Now, we will differentiate both sides with respect to x. Thus, we will get:
${{\left( \dfrac{dy}{dx} \right)}_{1}}=\dfrac{d}{dx}\left( \pm \sqrt{1-2x-{{x}^{2}}} \right)$
Here, we will used a differentiation formula:
$\dfrac{d}{dx}\sqrt{f\left( x \right)}=\dfrac{1}{2}\times \dfrac{f'\left( x \right)}{\sqrt{f\left( x \right)}}$
Thus, we have:
$\begin{aligned} & \Rightarrow {{\left( \dfrac{dy}{dx} \right)}_{1}}=\pm \left[ \dfrac{1}{2}\times \dfrac{-2-2x}{\sqrt{1-2x-{{x}^{2}}}} \right] \\\ & \Rightarrow {{\left( \dfrac{dy}{dx} \right)}_{1}}=\pm \left[ \dfrac{-1-x}{\sqrt{1-2x-{{x}^{2}}}} \right] \\\ \end{aligned}$
$\Rightarrow {{\left( \dfrac{dy}{dx} \right)}_{1}}=\pm \left[ \dfrac{x+1}{\sqrt{1-2x-{{x}^{2}}}} \right]$ …………………………….. (4)
Now, we have got the slope of tangent of the circle in (6). This slope should be equal to slope of the straight line $y-x-c=0$ . the slope of the line will be:
${{\left( \dfrac{dy}{dx} \right)}_{2}}=1$ ………………………………. (7)
Now ${{\left( \dfrac{dy}{dx} \right)}_{1}}$ and ${{\left( \dfrac{dy}{dx} \right)}_{2}}$ are equal so:
$\pm \left[ \dfrac{x+1}{\sqrt{1-2x-{{x}^{2}}}} \right]=1$
On squaring both sides, we get:
$\begin{aligned} & \dfrac{{{\left( x+1 \right)}^{2}}}{1-2x-{{x}^{2}}}={{\left( 1 \right)}^{2}} \\\ & \Rightarrow {{\left( x+1 \right)}^{2}}=1-2x-{{x}^{2}} \\\ & \Rightarrow {{x}^{2}}+2x+1=1-2x-{{x}^{2}} \\\ & \Rightarrow {{x}^{2}}+2x=-2x-{{x}^{2}} \\\ & \Rightarrow 2{{x}^{2}}+4x=0 \\\ & \Rightarrow {{x}^{2}}+2x=0 \\\ & \Rightarrow x\left( x+2 \right)=0 \\\ & \Rightarrow x=0\text{ and }x=-2 \\\ \end{aligned}$
Now, at $x=0$ , the slope of the tangent will be negative (seen from the graph), So $x=0$ . Now, we will put this value in the equation of the circle and we will find the value of u. Thus, we have:
$\begin{aligned} & {{0}^{2}}+{{y}^{2}}+2\left( 0 \right)-1=0 \\\ & \Rightarrow {{y}^{2}}=1 \\\ & \Rightarrow y=\pm 1 \\\ \end{aligned}$
At point $\left( 0,1 \right)$ , the slope is negative, but in our case slope =1 so $y=1$ is not possible. Hence, $y=-1$ . Thus we have:
$y=-1$
Now, we will put the values of x and y in the equation of line $y-x-c=0$ . Thus, we have:
$\begin{aligned} & -1-\left( 0 \right)-c=0 \\\ & \Rightarrow c=-1 \\\ \end{aligned}$
Hence, option (d) is correct.

Note: The above question can also be solved as follows:
As we know that, the circle and line touch each other at one point, we will substitute the value of $y-x+c$ as the equation of the circle, and then we will apply the condition for $D=0$ . Thus, we have:
${{x}^{2}}+{{\left( x+c \right)}^{2}}+2x+1=0\Rightarrow 2{{x}^{2}}+x\left( 2c+2 \right)+{{c}^{2}}-1=0$ . in above equation, we have only one value of x. so $D=0$ .
$\begin{aligned} & {{\left( 2c+2 \right)}^{2}}-4\left( {{c}^{2}}-1 \right)\left( 2 \right)=0 \\\ & \Rightarrow 4{{c}^{2}}+8c+4-4{{c}^{2}}+8=0 \\\ & \Rightarrow -4{{c}^{2}}+8c+12=0 \\\ & \Rightarrow {{c}^{2}}-2c-3=0 \\\ & \Rightarrow c=-1\text{ and }c=3 \\\ \end{aligned}$
We have $c=-1$ because c is negative.