Solveeit Logo
Login

Question

Question: The value of $\begin{vmatrix} \sqrt{6} & 2i & 3+\sqrt{6} \\ \sqrt{12} & \sqrt{3}+\sqrt{8}i & 3\sqrt...

The value of

∣62i3+6123+8i32+6i182+12i27+2i∣\begin{vmatrix} \sqrt{6} & 2i & 3+\sqrt{6} \\ \sqrt{12} & \sqrt{3}+\sqrt{8}i & 3\sqrt{2}+\sqrt{6}i \\ \sqrt{18} & \sqrt{2}+\sqrt{12}i & \sqrt{27}+2i \end{vmatrix} is

A

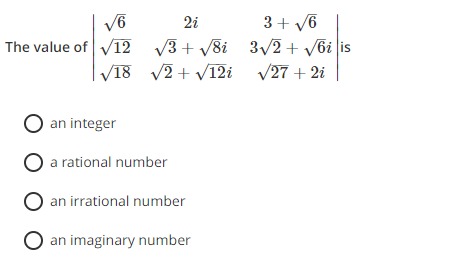
an integer

B

a rational number

C

an irrational number

D

an imaginary number

Answer

an integer

Explanation

Solution

The given determinant is: D=∣62i3+6123+8i32+6i182+12i27+2i∣D = \begin{vmatrix} \sqrt{6} & 2i & 3+\sqrt{6} \\ \sqrt{12} & \sqrt{3}+\sqrt{8}i & 3\sqrt{2}+\sqrt{6}i \\ \sqrt{18} & \sqrt{2}+\sqrt{12}i & \sqrt{27}+2i \end{vmatrix}

First, simplify the terms involving square roots: 12=4×3=23\sqrt{12} = \sqrt{4 \times 3} = 2\sqrt{3} 18=9×2=32\sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2} 8=4×2=22\sqrt{8} = \sqrt{4 \times 2} = 2\sqrt{2} 27=9×3=33\sqrt{27} = \sqrt{9 \times 3} = 3\sqrt{3}

Substitute these simplified terms into the determinant: D=∣62i3+6233+22i32+6i322+23i33+2i∣D = \begin{vmatrix} \sqrt{6} & 2i & 3+\sqrt{6} \\ 2\sqrt{3} & \sqrt{3}+2\sqrt{2}i & 3\sqrt{2}+\sqrt{6}i \\ 3\sqrt{2} & \sqrt{2}+2\sqrt{3}i & 3\sqrt{3}+2i \end{vmatrix}

Perform row operations to simplify the determinant. Apply R2→R2−2R1R_2 \to R_2 - \sqrt{2} R_1 and R3→R3−3R1R_3 \to R_3 - \sqrt{3} R_1. For R2→R2−2R1R_2 \to R_2 - \sqrt{2} R_1: The first element: 23−2(6)=23−12=23−23=02\sqrt{3} - \sqrt{2}(\sqrt{6}) = 2\sqrt{3} - \sqrt{12} = 2\sqrt{3} - 2\sqrt{3} = 0. The second element: (3+22i)−2(2i)=3+22i−22i=3(\sqrt{3}+2\sqrt{2}i) - \sqrt{2}(2i) = \sqrt{3}+2\sqrt{2}i - 2\sqrt{2}i = \sqrt{3}. The third element: (32+6i)−2(3+6)=32+6i−32−12=6i−23(3\sqrt{2}+\sqrt{6}i) - \sqrt{2}(3+\sqrt{6}) = 3\sqrt{2}+\sqrt{6}i - 3\sqrt{2} - \sqrt{12} = \sqrt{6}i - 2\sqrt{3}. So, the new second row is (0,3,6i−23)(0, \sqrt{3}, \sqrt{6}i - 2\sqrt{3}).

For R3→R3−3R1R_3 \to R_3 - \sqrt{3} R_1: The first element: 32−3(6)=32−18=32−32=03\sqrt{2} - \sqrt{3}(\sqrt{6}) = 3\sqrt{2} - \sqrt{18} = 3\sqrt{2} - 3\sqrt{2} = 0. The second element: (2+23i)−3(2i)=2+23i−23i=2(\sqrt{2}+2\sqrt{3}i) - \sqrt{3}(2i) = \sqrt{2}+2\sqrt{3}i - 2\sqrt{3}i = \sqrt{2}. The third element: (33+2i)−3(3+6)=33+2i−33−18=2i−32(3\sqrt{3}+2i) - \sqrt{3}(3+\sqrt{6}) = 3\sqrt{3}+2i - 3\sqrt{3} - \sqrt{18} = 2i - 3\sqrt{2}. So, the new third row is (0,2,2i−32)(0, \sqrt{2}, 2i - 3\sqrt{2}).

The determinant becomes: D=∣62i3+6036i−23022i−32∣D = \begin{vmatrix} \sqrt{6} & 2i & 3+\sqrt{6} \\ 0 & \sqrt{3} & \sqrt{6}i - 2\sqrt{3} \\ 0 & \sqrt{2} & 2i - 3\sqrt{2} \end{vmatrix}

Expand the determinant along the first column: D=6∣36i−2322i−32∣−0+0D = \sqrt{6} \begin{vmatrix} \sqrt{3} & \sqrt{6}i - 2\sqrt{3} \\ \sqrt{2} & 2i - 3\sqrt{2} \end{vmatrix} - 0 + 0

Now, evaluate the 2x2 determinant: ∣36i−2322i−32∣=3(2i−32)−2(6i−23)\begin{vmatrix} \sqrt{3} & \sqrt{6}i - 2\sqrt{3} \\ \sqrt{2} & 2i - 3\sqrt{2} \end{vmatrix} = \sqrt{3}(2i - 3\sqrt{2}) - \sqrt{2}(\sqrt{6}i - 2\sqrt{3}) =23i−36−(12i−26)= 2\sqrt{3}i - 3\sqrt{6} - (\sqrt{12}i - 2\sqrt{6}) =23i−36−(23i−26)= 2\sqrt{3}i - 3\sqrt{6} - (2\sqrt{3}i - 2\sqrt{6}) =23i−36−23i+26= 2\sqrt{3}i - 3\sqrt{6} - 2\sqrt{3}i + 2\sqrt{6} =−36+26=−6= -3\sqrt{6} + 2\sqrt{6} = -\sqrt{6}

Now, multiply by the factor 6\sqrt{6}: D=6×(−6)=−(6)2=−6D = \sqrt{6} \times (-\sqrt{6}) = -(\sqrt{6})^2 = -6.

The value of the determinant is -6.

Therefore, the answer is an integer.