Question

The value of ‘a’ for which $a{{x}^{2}}+{{\sin }^{-1}}\left( {{x}^{2}}-2x+2 \right)+{{\cos }^{-1}}\left( {{x}^{2}}-2x+2 \right)=0$ has real solution is.

Answer 1

Hint: We will write $\left( {{x}^{2}}-2x+2 \right)$ as ${{\left( x-1 \right)}^{2}}+1$. We know that the value of sin varies from -1 to 1, thus we will get, $-1\le {{\left( x-1 \right)}^{2}}+1\le 1$. We will solve this further to get x=1. In the final step, we will put x=1 in the given equation to get the value of ‘a’.

Complete step-by-step answer:
It is given in the question that we have to find the value of ‘a’ for which $a{{x}^{2}}+{{\sin }^{-1}}\left( {{x}^{2}}-2x+2 \right)+{{\cos }^{-1}}\left( {{x}^{2}}-2x+2 \right)=0$ has real solution.
We can write $\left( {{x}^{2}}-2x+2 \right)$ as $\left[ {{x}^{2}}-2\left( x \right)\left( 1 \right)+1 \right]+1$, so we will get, ${{\left( x-1 \right)}^{2}}+1$.
We know that the value of sin varies from -1 to 1. So, we can represent it graphically as follows.

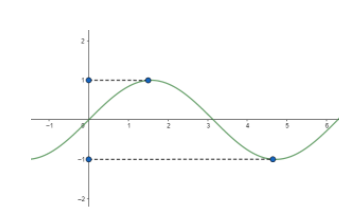
So, from this we can limit ${{\left( x-1 \right)}^{2}}+1$ between -1 and 1. So, we can write it as,
$-1\le {{\left( x-1 \right)}^{2}}+1\le 1$
But we know that ${{\left( x-1 \right)}^{2}}+1$ is already greater than 1, so in order to satisfy $-1\le {{\left( x-1 \right)}^{2}}+1\le 1$, we have to make the term ${{\left( x-1 \right)}^{2}}+1$ equal to 1, so we get,
${{\left( x-1 \right)}^{2}}+1=1$
We know that ${{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}$, so we get,
${{x}^{2}}-2x+2=1$
On transposing 1 from RHS to LHS, we get,
$\begin{aligned} & {{x}^{2}}-2x+2-1=0 \\\ & {{x}^{2}}-2x+1=0 \\\ \end{aligned}$
We can write -2x as –x –x, so we will get,
$\begin{aligned} & {{x}^{2}}-x-x+1=0 \\\ & x\left( x-1 \right)-1\left( x-1 \right)=0 \\\ & \left( x-1 \right)\left( x-1 \right)=0 \\\ & x=1 \\\ \end{aligned}$
On putting the value of x as 1 in the equation $a{{x}^{2}}+{{\sin }^{-1}}\left( {{x}^{2}}-2x+2 \right)+{{\cos }^{-1}}\left( {{x}^{2}}-2x+2 \right)=0$, we get,
$\begin{aligned} & a{{\left( 1 \right)}^{2}}+{{\sin }^{-1}}\left( {{1}^{2}}-2\left( 1 \right)+2 \right)+{{\cos }^{-1}}\left( {{1}^{2}}-2\left( 1 \right)+2 \right)=0 \\\ & a+{{\sin }^{-1}}\left( 1 \right)+{{\cos }^{-1}}\left( 1 \right)=0 \\\ \end{aligned}$
We know that, ${{\sin }^{-1}}\left( 1 \right)=\dfrac{\pi }{2}$ and ${{\cos }^{-1}}\left( 1 \right)=0$.
So, we can substitute these values in the equation, so we will get,
$\begin{aligned} & a+\dfrac{\pi }{2}+0=0 \\\ & a+\dfrac{\pi }{2}=0 \\\ \end{aligned}$
On transposing $\dfrac{\pi }{2}$ from the LHS to the RHS, we get,
$a=-\dfrac{\pi }{2}$
Thus, the value of ‘a‘ is $-\dfrac{\pi }{2}$.

Note: Most of the students make mistake while taking the value of ${{\sin }^{-1}}\left( 1 \right)$ and ${{\cos }^{-1}}\left( 1 \right)$. They may take ${{\sin }^{-1}}\left( 1 \right)$ as 0 and ${{\cos }^{-1}}\left( 1 \right)$ as $\dfrac{\pi }{2}$. They may get the exact same answer, that is $-\dfrac{\pi }{2}$ but the solution is wrong conceptually and due to this they may get less marks.