Question
Question: The value of $9999 \int_{0}^{\infty} \frac{dx}{(x+\sqrt{1+x^2})^{100}}$ is _____....
The value of 9999∫0∞(x+1+x2)100dx is _____.
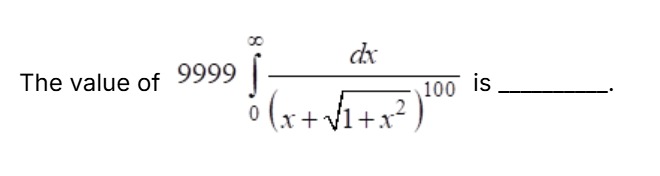
100
Solution
The problem requires evaluating a definite integral involving the term x+1+x2. This form suggests using a hyperbolic substitution.
Let x=sinht.
Then, dx=coshtdt.
Also, 1+x2=1+sinh2t=cosh2t=cosht (since x≥0, t≥0, so cosht>0).
Substitute these into the term (x+1+x2):
x+1+x2=sinht+cosht=et.
Now, change the limits of integration:
When x=0, sinht=0⟹t=0.
When x→∞, sinht→∞⟹t→∞.
Substitute everything into the integral I=∫0∞(x+1+x2)100dx:
I=∫0∞(et)100coshtdt
I=∫0∞e100tcoshtdt
I=∫0∞cosht⋅e−100tdt
Recall the definition of cosht=2et+e−t.
I=∫0∞2et+e−te−100tdt
I=21∫0∞(et⋅e−100t+e−t⋅e−100t)dt
I=21∫0∞(e−99t+e−101t)dt
Now, integrate term by term:
∫e−atdt=−a1e−at.
I=21[−991e−99t−1011e−101t]0∞
Evaluate the definite integral using the limits:
As t→∞, e−99t→0 and e−101t→0.
At t=0, e−99(0)=1 and e−101(0)=1.
I=21[(0−0)−(−991(1)−1011(1))]
I=21[0−(−991−1011)]
I=21(991+1011)
I=21(99×101101+99)
I=21(9999200)
I=9999100
The question asks for the value of 9999∫0∞(x+1+x2)100dx, which is 9999I.
9999I=9999×9999100=100.
