Question
Question: The value of $17cot(cosec^{-1}\frac{5}{3}+tan^{-1}\frac{2}{3})$ is _____....
The value of 17cot(cosec−135+tan−132) is _____.
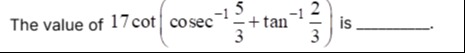
6
Solution
Let the given expression be E. We have E=17cot(cosec−135+tan−132).
First, we evaluate the term inside the cotangent function. Let A=cosec−135. This implies cosecA=35. Since cosecA=sinA1, we have sinA=53. We can convert sin−153 to tan−1. Consider a right triangle with the opposite side 3 and the hypotenuse 5. The adjacent side is 52−32=25−9=16=4. Thus, tanA=adjacentopposite=43. So, cosec−135=sin−153=tan−143.
Now, the expression inside the cotangent function is tan−143+tan−132. We use the formula for the sum of two inverse tangents: tan−1x+tan−1y=tan−1(1−xyx+y), provided xy<1. Here x=43 and y=32. The product xy=43×32=126=21. Since xy=21<1, we can use the formula: tan−143+tan−132=tan−1(1−43×3243+32)=tan−1(1−126129+8)=tan−1(211217). Simplifying the fraction: 211217=1217×2=617. So, cosec−135+tan−132=tan−1617.
The expression E becomes 17cot(tan−1617). We know that cot(θ)=tan(θ)1. So, cot(tan−1x)=tan(tan−1x)1=x1 for x=0. Here x=617, which is not zero. cot(tan−1617)=6171=176.
Finally, we substitute this value back into the expression for E: E=17×cot(tan−1617)=17×176. E=6.
