Question

The value for crystal field stabilisation energy is zero for:
(A) ${ K }_{ 2 }\left[ Mn{ F }_{ 6 } \right]$
(B) ${ K }_{ 3 }\left[ Fe(CN)_{ 6 } \right]$
(C) ${ K }_{ 3 }\left[ Fe{ F }_{ 6 } \right]$
(D) ${ K }_{ 4 }\left[ Fe(CN)_{ 6 } \right]$

Answer 1

Hint: Crystal field stabilization energy: Crystal field stabilization energy is the energy of electronic configuration in the ligand field - Electronic configuration in the isotropic field.

Complete answer step-by-step:

The splitting pattern in each complex compound is octahedral. If a strong field ligand is present, then back pairing will take place as in the case of B and D, and splitting energy can never be zero, since no electron can go into ${ e }_{ g }$ orbitals.
But if a strong field is not present, then back pairing will not take place as in the case of A and C.
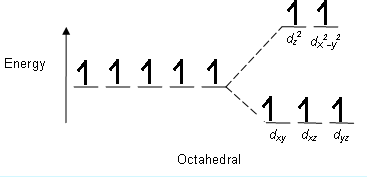
The splitting pattern in ${ K }_{ 3 }\left[ Fe{ F }_{ 6 } \right]$ is;

Atomic number of Fe = ${ 26 }$
Electronic configuration = $\left[ Ar \right] { 3d }^{ 6 }{ 4s }^{ 2 }$
For, ${ Fe }^{ +3 } = \left[ Ar \right] { 3d }^{ 5 } or { t }_{ 2g }^{ 3 }{ e }_{ g }^{ 2 }$
The crystal field splitting energy for octahedral complexes are given by;
CFSE = ${ -0.4\times }{ t }_{ 2g }{ +0.6\times }{ e }_{ g }$
By putting the values, we get
CFSE = ${ -0.4\times 3 }{ +0.6\times 2 }$
CFSE = 0
Now, for ${ K }_{ 2 }\left[ Mn{ F }_{ 6 } \right]$
Atomic number of Mn = ${ 25 }$
Electronic configuration = $\left[ Ar \right] { 3d }^{ 5 }{ 4s }^{ 2 }$
For, ${ Mn }^{ +3 } = \left[ Ar \right] { 3d }^{ 4 }or { t }_{ 2g }^{ 3 }{ e }_{ g }^{ 1 }$
The crystal field splitting energy for octahedral complexes are given by;
CFSE = ${ -0.4\times }{ t }_{ 2g }{ +0.6\times }{ e }_{ g }$
By putting the values, we get
CFSE = ${ -0.4\times 3 }{ +0.6\times 1 }$
CFSE = ${ -0.6 } \Delta _{ 0 }$
Hence, we can say that the value for crystal field stabilization energy is zero for ${ K }_{ 3 }\left[ Fe{ F }_{ 6 } \right]$.
The correct option is C.

Note: The possibility to make a mistake is that you may use the crystal field splitting energy formula for tetrahedral, not octahedral. But all the compounds are octahedral so do not confuse between them.