Question
Question: The \(v-x\) curve for a car in a race on a straight line is given, identifying the correct \(a-x\) g...
The v−x curve for a car in a race on a straight line is given, identifying the correct a−x graph.

A. 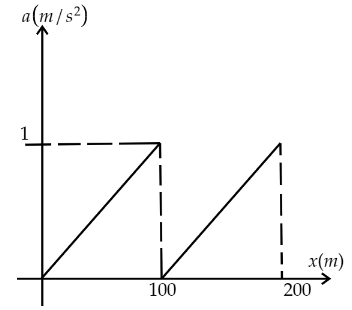
B. 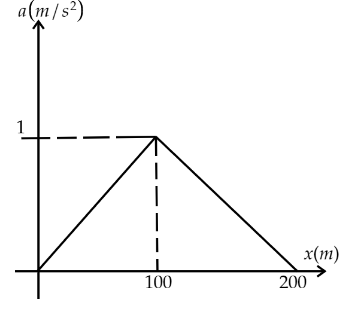
C. 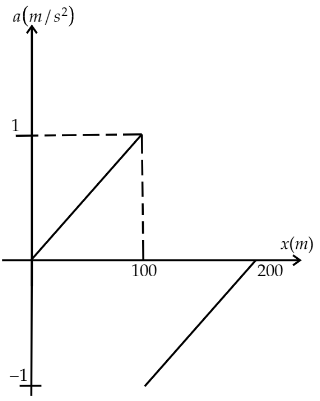
D. 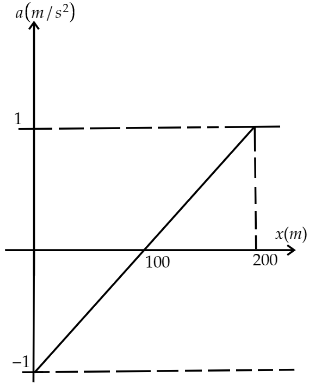
Solution
The velocity of a particle is the rate of change of displacement with time and acceleration of a particle is the rate of change of velocity with time. Use the definition to find the relation between the velocity and displacement and the relation between the acceleration and displacement.
Formula used:
The equation of a straight line is given by the formula,
y=mx+c
where, m is the slope of the straight line c is the intercept on the y axis.
The instantaneous velocity of a particle is given by,
v=dtdx
where, x is the displacement of the particle t is the time.
The instantaneous acceleration of a particle is given by,
a=dtdv
where, is the v velocity of the particle and is the time.
Complete step by step answer:
We know that the velocity of a particle is the rate of change of displacement with time and the acceleration of a particle is the rate of change of velocity with time. The formula for instantaneous velocity is given by, v=dtdx, where, xis the displacement of the particle t is the time. And the formula for instantaneous acceleration is given by, a=dtdv where, is the v velocity of the particle and is the time.
Now, in the curve we first have to find the relation between the velocity and the displacement of the car. We can find the relation using the equation of straight line as the curve is a straight line. So, from the curve we can see that for 0 to 100 the slope of the curve is m=10010=101 and the intercept on the y axis is zero. So, equation for 0 to 100 is, v=101x ………( i)
So, differentiating with respect to time we have,
dtdv=101dtdx
⇒a=101v
Putting the value of equation (i) again we have,
a=1001x
This shows that the a-x curve will be straight line of slope 1001
Now, for 100 to 200 the slope of the curve is −101as the angle is negative and the intercept on the v axis is at 20.
So the equation of the curve is, v=20−101x………( ii)
So, differentiating with respect to time we have,
dtdv=−101dtdx
a=−101v
Putting the value of equation (ii) again we have,
a=−2+1001x
Hence, the curve will be a straight line of slope 1001 with an intercept at a axis at −2. So, the a-x curve can be drawn as given below.
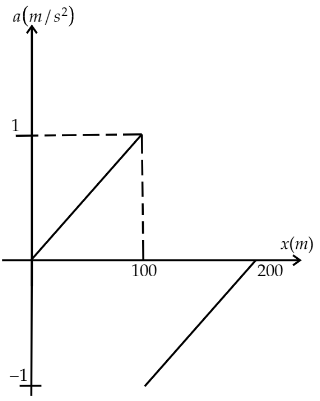
Hence, option C is the correct answer.
Note: Always remember that since there is no direct relation between velocity and displacement or velocity and acceleration so we have to deduce the relation from the graph given then from there it is easy to find any relation as asked.
