Question
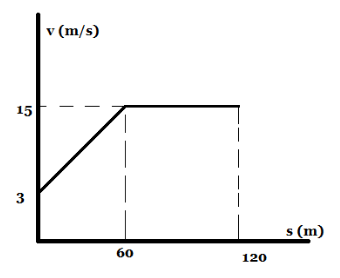
Question: The \( v - s \) graph describing the motion of a motorcycle is shown in the figure. The time needed ...
The v−s graph describing the motion of a motorcycle is shown in the figure. The time needed for the motorcycle to reach the position s=120m [Given that ln5=1.6 ] is 2xsec , find x ?
Solution
Here we find the relation between the velocity v and the displacement s for the two curves separately. For the first half of the journey till s=60m we will formulate the equation of the curve as v=5s+3 . For the second half of the journey from s=60m to s=120m , we see that v=15m/s . In both these equations, we will substitute v=dtds and solve the integrations with appropriate limits.
Formula used:
v=dtds
Complete Step by step solution:
From the graph, we form the relationship between the velocity v and the displacement s for the first half of the journey, i.e. from s=0m to s=60m .
The slope of the graph can be determined by dividing the Y axis coordinates with the X axis coordinates. Thus we get the slope as
60−015−3=51
Now considering the general Y axis coordinate as v and the X axis coordinate as s the equation of the line in slope point form will be
s−0v−3=51
⇒v=5s+15
We know that
v=dtds
Substituting the value of v from the above equation, we get
dtds=5s+15
⇒s+15ds=5dt
Now integrating both sides of the equation, we get,
⇒∫s+15ds=∫5dt
Putting the limits of integration from s=0m to s=60m , we get,
⇒s=0∫s=60s+15ds=t=0∫t=t5dt
⇒[ln(s+15)]060=[5t]0t
Putting the values of the limits of the integration, we get,
⇒[ln(60+15)−ln(0+15)]=[5t−50]
⇒[ln(75)−ln(15)]=5t
On further simplifying, we get,
⇒5t=ln(1575)
⇒5t=ln(5)
⇒t=5×ln(5)
It is given in the question that ln5=1.6 . Substituting this value in the above equation, we get,
⇒t=5×1.6
⇒t=8sec
This is the time taken for the motorcycle to reach s=60m .
Now for the next half of the journey, i.e. from s=60m to s=120m , we can repeat the above process.
We see that the velocity for this half of the journey is constant, i.e. v=15m/s .
Using this uniform velocity, and the relation v=dtds , we get,
v=15m/s=dtds
⇒dtds=15
⇒ds=15dt
Integrating both sides, we get,
⇒∫ds=∫15dt
We now have to substitute the limits carefully. The displacement s will vary from s=60m to s=120m . The time taken t will vary from t=8sec to t=t , such that the value of the time t will give the actual time taken by the motorcycle to travel the entire distance of 120m .
⇒s=60∫s=120ds=t=8∫t=t15dt
⇒[s]60120=[15t]8t
Now calculating the limits properly, we obtain,
⇒[15(t−8)]=[120−60]
⇒t−8=1560
Upon rearranging the equation we get,
⇒t=8+4
⇒t=12sec
It is given that this time is equal to 2x .
Therefore 2x=12sec .
⇒x=6
Thus the total time taken by the motorcycle to travel the entire distance of 120m is 12sec with the value of x being 6 .
Note:
The motorcycle moves with some acceleration in the first half of the motion. In the second half of the motion, the acceleration of the motorcycle is 0 . Since the two graphs are two separate straight lines, we have analyzed them differently and have used the major relation v=dtds to simplify and integrate to get the solution.
