Question
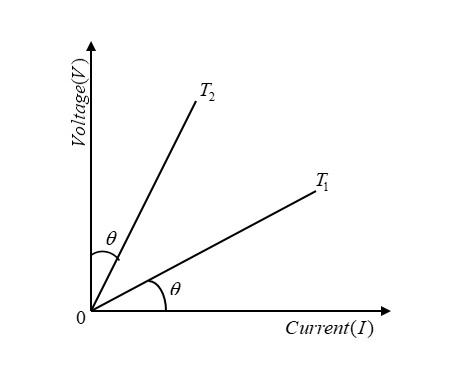
Question: The V - I graph for a conductor at temperature \({T_1}\) and \({T_2}\) are as shown in the figure. T...
The V - I graph for a conductor at temperature T1 and T2 are as shown in the figure. The term (T2−T1) is proportional to:
A) sin2θsin2θ
B) sin2θcot2θ
C) sin2θcos2θ
D) sin2θtan2θ
Solution
Recall that the slope of V−I graph gives R . Revise the trigonometric formulae for the ease of calculations in the question. Also, we must know how the resistance varies with respect to temperature.
Complete step by step solution:
Here we are given a V−I graph.
By Ohm’s law, we know that: V∝I
⇒V=IR
⇒IV=R
⇒ The slope of V−I graph gives R
∴ Consider I1V1=R1 resistance at temperature T1 and I2V2=R2 resistance at temperature T2 . self-made diagram
But, we also know that
tanθ=adjacentopposite
⇒tanθ=I1V1
⇒R1=tanθ
And R2=tan(90∘−θ)
⇒R2=cotθ
The resistance of a conductor always depends on the temperature. As the temperature increases the resistance of the conductor also increases. For small temperatures, the resistance of the conductor increases linearly with temperature, which is given by the equation:
R=Ro(1+αT)
Where R is resistance at temperature T in Ohms(Ω)
Ro is resistance at absolute temperature in Ω
T is temperature in Kelvin(K)
α is temperature coefficient of resistance
∴R1=Ro(1+αT1) and R2=Ro(1+αT2)
Now,
R2−R1=Ro[1+α(T2−T1)]
But R2=cotθ and R1=tanθ
Substituting these values in the above equation, we get
cotθ−tanθ=Ro[1+α(T2−T1)]
⇒T2−T1∝cotθ−tanθ equation(1)
Now, we need to simply the equation cotθ−tanθ
cotθ−tanθ=sinθcosθ−cosθsinθ
⇒cotθ−tanθ=sinθ×cosθcosθ×cosθ−sinθ×sinθ
⇒cotθ−tanθ=sinθcosθcos2θ−sin2θ
Now, we can substitute cos2θ−sin2θ=cos2θ
⇒cotθ−tanθ=sinθcosθcos2θ
Now multiplying the numerator and denominator by 2 , we get:
⇒cotθ−tanθ=2sinθcosθ2cos2θ
We know that 2sinθcosθ=sin2θ
∴cotθ−tanθ=sin2θ2cos2θ
Substituting this value in equation(1)
⇒T2−T1∝sin2θ2cos2θ
⇒T2−T1∝sin2θcos2θ (∵2 is an integer we can ignore it)
∴ Option (C),sin2θcos2θ is the correct option.
Note: One must know that the resistance of the conductor for small temperatures increases with increase in temperature. One is very likely to forget the trigonometric formulas. Do not confuse or make mistakes in the trigonometric formulas of cos2θ,sin2θ.
