Question

The upper part of the tree broken by the wind which makes an angle of $60^\circ$ with the ground and the distance from the roots to the point where the top of the tree meets the ground is $20{\text{m}}$. Find the length of the broken part of the tree.

Answer 1

Here, we will use the concept of trigonometry by drawing a triangle from the given information. Where a tree is standing from the point which is our perpendicular of the triangle. Also, the base of the triangle will be the distance of that tree on the ground and where the broken part of the tree meets the ground and the Hypotenuse of the triangle will be the broken part of the tree. We will use the formula $\cos \theta = \dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}}$.

Complete step-by-step answer:
Step 1: First of all, we will draw the triangle where ${\text{A}}$ is a tree which falls from a point ${\text{B}}$ to the ground with an angle of $60^\circ$ at the point ${\text{C}}$ :

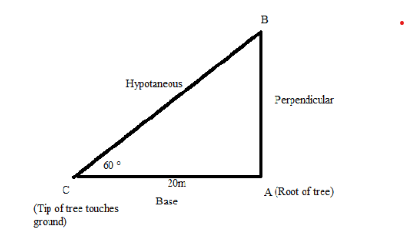
Step 2: We can see from the above diagram that it makes a right-angle triangle where, ${\text{AB}} = {\text{Perpendicular}}$, ${\text{AC}} = {\text{Base}} = 20{\text{m}}$ and ${\text{BC}} = {\text{Hypotenuse}}$.
Step 3: Now by using the formula for $\cos \theta = \dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}}$:
$\cos \theta = \dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}} = \dfrac{{{\text{AC}}}}{{{\text{BC}}}}{\text{ (}}\because {\text{as given in step 2)}}$…………….. (1)
The value of the angle $\angle {\text{ACB = 6}}{{\text{0}}^o}$also ${\text{AC}} = 20{\text{m}}$ so, by putting these values in the above expression (1):
$\Rightarrow \cos {60^o} = \dfrac{{{\text{AC}}}}{{{\text{20}}}}$
Step 4: We know that, the value of $\cos {60^o} = \dfrac{1}{2}$, substituting this value in $\cos {60^o} = \dfrac{{{\text{AC}}}}{{{\text{20}}}}$ :
$\Rightarrow \dfrac{1}{2} = \dfrac{{{\text{AC}}}}{{{\text{20}}}}$
By taking $20$in the LHS side and $2$in RHS:
$\Rightarrow 20 = 2{\text{AC}}$
By dividing the LHS side by $2$:
$\Rightarrow \dfrac{{20}}{2} = {\text{AC}}$
Thus, solving for ${\text{AC}}$:
$\Rightarrow {\text{AC}} = 10$

So, the length of the broken part of the tree is: ${\text{AC = 10m}}$.

Note: Students should always take the side opposite to the angle as perpendicular and then write the value for corresponding trigonometric functions.
Students should not confuse between sine and cosine value for $60^\circ$, below are the values for sine, cosine and tan which students should remember:

| ${0^0}$| ${30^0}$| ${45^0}$| ${60^0}$| ${90^0}$
---|---|---|---|---|---
sin| $0$| $\dfrac{1}{2}$| $\dfrac{{\sqrt 2 }}{2}$| $\dfrac{{\sqrt 3 }}{2}$| $1$
cos| $1$| $\dfrac{{\sqrt 3 }}{2}$| $\dfrac{{\sqrt 2 }}{2}$| $\dfrac{1}{2}$| $0$
tan| $0$| $\dfrac{{\sqrt 3 }}{3}$| $1$| $\sqrt 3$| Undefined