Question

The upper half of an inclined plane with inclination $\phi$ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half is given by-
(A). $2\tan \phi$
(B). $\tan \phi$
(C). $2\sin \phi$
(D). $2\cos \phi$

Answer 1

The first part of the inclined plane is smooth so o frictional force will act when the body moving through the upper half but lower half is rough due to which frictional force comes into play. Draw a FBD diagram of the body and resolve the forces into its components. Solve forces acting in different directions on the body. Using equations of motion and Newton’s second law, we can calculate the coefficient of friction.

Formula used:
$mg\sin \phi =ma$
${{v}^{2}}={{u}^{2}}+2as$
$mg\sin \phi -\mu mg\cos \phi =ma$

Complete answer:
Given, a body is coming down an inclined plane inclined at an angle $\phi$. The upper half is smooth while the lower half is rough. The FBD diagram tells us about the different forces acting on a system.
The FBD diagram for the body will be-

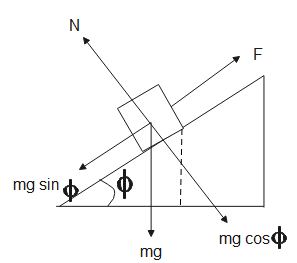
In the figure shown, the body is halfway through the inclined plane, let the length of the incline be $l$. The first half of the plane is smooth. Therefore, the force acting when the body comes down the first half is-
$\begin{aligned} & mg\sin \phi =ma \\\ & \Rightarrow a=g\sin \phi \\\ \end{aligned}$
The acceleration of the body in the first half is $g\sin \phi$.
Applying equation of motion-
${{v}^{2}}={{u}^{2}}+2as$ - (1)
Here, $v$ is the final velocity
$u$ is the initial velocity
$a$ is the acceleration
$s$is the displacement
Substituting values in the above equation, we get,
$\begin{aligned} & {{v}^{2}}=0+2g\sin \phi \dfrac{l}{2} \\\ & \Rightarrow v=\sqrt{2g\sin \phi \dfrac{l}{2}} \\\ \end{aligned}$
Therefore, the velocity of the body just before it starts moving through the second half is $\sqrt{2g\sin \phi \dfrac{l}{2}}$.
In the second half, the forces acting on the body will be-
$mg\sin \phi -\mu N=ma$
Here, $\mu N$ is the frictional force. $\mu$ is the coefficient of friction while $N$ is the normal force.
From the figure, $N=mg\cos \phi$
Substituting in the above equation, we get,
$\begin{aligned} & mg\sin \phi -\mu mg\cos \phi =ma \\\ & \Rightarrow a=g\sin \phi -\mu g\cos \phi \\\ \end{aligned}$
Therefore, the acceleration of the body when it is coming down the second half is $g\sin \phi -\mu g\cos \phi$. Substituting given values in eq (1), we get,
$\begin{aligned} & 0=2g\sin \phi \dfrac{l}{2}+2(g\sin \phi -\mu g\cos \phi )\dfrac{l}{2} \\\ & \Rightarrow 0=\sin \phi +\sin \phi -\mu \cos \phi \\\ & \Rightarrow \mu \cos \phi =2\sin \phi \\\ & \therefore \mu =2\tan \phi \\\ \end{aligned}$
Therefore, the value of coefficient of friction is $2\tan \phi$.
For the lower half, the coefficient of friction is $2\tan \phi$.

Hence, the correct option is (A).

Note:
According to Newton’s second law of motion, a body undergoes acceleration when there is external force acting on it otherwise it moves with uniform motion or remains at rest. The force that opposes the motion of a body is frictional force. Since, the upper half is smooth, no frictional force acts on the body, the lower half is rough and interlocking of irregularities takes place due to which frictional force comes into play.