Question

The upper half of an inclined plane of inclination $\theta$ is perfectly smooth while the lower half is rough. A block starting from rest at the top of the plane will again come to rest at the bottom, if the coefficient of friction between the block and lower half of the plane is given by:
A. $2 \theta$
B. $2 tan \theta$
C. $2 cos \theta$
D. $2 sin \theta$

Answer 1

Remember that friction plays no role over smooth surfaces. Also, if a block starts at rest and ends up at rest what will be the change in its kinetic energy? Recall that the change in kinetic energy is equivalent to the work done, and using this determine the work done by the frictional and gravitational forces respectively. Do not forget to select only the contributing components of your force and displacement vectors.

Formula used:
Work done = Force $\times$ Displacement = $\vec{F}\;.\vec{S}$

Complete step-by-step answer:
Let us first understand the different components to the problem.
We have a block placed at the top of an inclined plane. Let the length of the inclined plane be $L$. The upper half of the inclined plane is smooth while the lower half of the plane is rough, i.e., lengths of the smooth and rough surfaces = $\dfrac{L}{2}$ each.
Now, since the block is starting from rest from the top and ends up again at rest at the bottom,
Work done $\Delta KE = 0 \Rightarrow W = 0$ since initial and final velocities are zero.

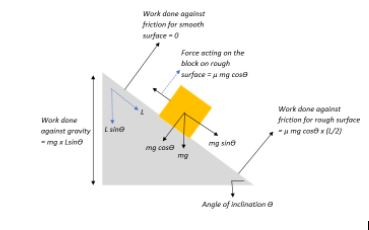
In the whole picture there are two kinds of contributing forces to work: frictional force and gravitational force. Therefore, we need to find out

A. Work done by frictional force $W_{friction}$:
Since the perfectly smooth surface entails no frictional force we take $W_{smooth} = 0$.
However, for the rough surface the frictional force is a contributor and hence we need to find $W_{rough}$
$W_{rough} = F_{frictional} \times S_{rough}$ where $S$ is the displacement of the block over the length of the rough surface and $F_{frictional}$ is the frictional force acting on the block. Now, the the component of force contributing to the frictional force is the normal reaction acting on the block, i.e.,
Normal reaction $N = mg cos \theta \Rightarrow F_{frictional} = \mu mg cos \theta$ where $\mu$ is the co-efficient of friction.
We know that $S_{rough} = \dfrac{L}{2}$
Hence, $W_{rough} = F_{frictional} \times S_{rough} \Rightarrow W_{rough} = \mu mg cos \theta \times \dfrac{L}{2}$
Therefore $W_{friction} = W_{smooth} + W_{rough} = 0 + \mu mg cos \theta \times \dfrac{L}{2} = \mu mg cos \theta \times \dfrac{L}{2}$
However, since frictional force opposes the relative motion of the block, work done by friction becomes negative. Therefore,
$W_{friction} = -\; \mu mg cos \theta \times \dfrac{L}{2}$

B. Work done by gravity
We have $W_{gravity} = F_{gravity} \times S_{gravity}$
The gravitational force acting on the block is straightforwardly given as $F_{gravity} = mg$
However, the gravity acting on the block acts along the component of displacement that is perpendicular to the motion of the block, i.e.,
$S_{gravity} = L sin \theta$
Therefore,
$W_{gravity} = F_{gravity} \times S_{gravity} \Rightarrow W_{gravity} = mg \times L sin \theta$
Since the object goes down the inclination which contributes to increasing KE, the work done by gravity here remains positive.
Now, from $W = 0$ that we established in the beginning, we get:
$W_{friction} + W_{gravity} = 0$
$\Rightarrow -\; \mu mg cos \theta \dfrac{L}{2} + mg \times L sin \theta = 0$
$\Rightarrow -\; \mu mg cos \theta \dfrac{L}{2} = -\;mgL\; sin \theta$
$\Rightarrow \mu = 2\;\dfrac{sin \theta}{cos \theta} \Rightarrow \mu = 2 tan \theta$

So, the correct answer is “Option B”.

Note: It is very important to remember to separate the components of forces and choose the correctly contributing component for each direction. The same applies for the direction of displacement since frictional force acts along the whole half length of the inclination whereas gravity acts in the vertically downward direction which is the $sin \theta$ component of the length of the inclination. Also, do not forget to include the coefficient of friction while determining the frictional force.
It is also crucial to remember the sign convention for work done. If any force retards the motion of a body, the work done by that force will be negative but if a force contributes to the motion of the body the work done by that force will be positive. Similarly, if the kinetic energy increases the work done by that force will be positive and if there is a loss of kinetic energy the work done by that force will be negative.