Question

The upper end of the string of a simple pendulum is fixed to a vertical z-axis and set in motion such that the bob moves along a horizontal circular path of radius 2m, parallel to the xy plane, 5m above the origin. The bob has a speed of 3m/s. The string breaks when the bob is vertically above the x-axis, then it lands on the xy plane at a point (x,y).

A. x=2m
B. $x\rangle 2m$
C. y=3m
D. y=5m

Answer 1

As a very step, you could read the question very carefully and thus find the coordinate of the bob at the moment that the string broke. From there you will get the x coordinate. Now consider the projectile motion that the bob undergoes after that and use the equation of motion to find the horizontal range (y) accordingly.
Formula used:
Equation of motion,
$s=ut+\dfrac{1}{2}a{{t}^{2}}$

Complete answer:
In the question, we are given a simple pendulum that is fixed to a vertical z-axis undergoing circular motion as shown in the figure. The speed of the bob is given as 3m/s. As per the given conditions we could say that the coordinates of the given simple pendulum when the string breaks would be (2,0,5) and the initial vertical velocity would be zero. So for vertical motion,
$s=ut+\dfrac{1}{2}a{{t}^{2}}$
$\Rightarrow 5=0-\dfrac{1}{2}g{{t}^{2}}$
$\Rightarrow {{t}^{2}}=1$
$\Rightarrow t=\pm 1$
So, the time taken for the ball to fall to the xy plane would be 1 second.
Now the horizontal distance travelled by the bob which is otherwise called the range of the projectile motion would be,
$s=ut$
Here, u is the horizontal initial velocity 3m/s.
$\therefore s=3\times 1=3m$
So the projectile motion could be depicted as,

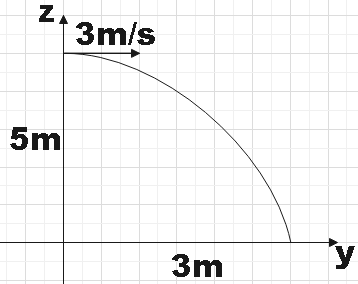
We found the (x,y) to be (2,3).

Hence A and C are correct options.

Note:
In questions like these where you are dealing with coordinates chances there that you get confused between axes. So, one should get help by making a neat diagram that depicts the exact situation and thereby avoid such unnecessary confusions. Also, make sure to assign the signs for parameters correctly.