Question

The two identical wires of iron and copper with their Young’s modulus with ratio 3:1 are suspended at the same level. They are to be loaded so as to have the same extension and hence, level. Ratio of its weight is
(a) 1:3
(b) 2:1
(c) 3:1
(d) 4:1

Answer 1

We will use the formula for stress and strain of an object and after taking the ratio of stress to the strain we will get the formula for Young’s Modulus. This will be helpful in finding the weights of iron and copper which are suspended at the same level and have the same extension.

Formula used: $Stress=\dfrac{F}{A},Strain=\dfrac{{{L}_{\left( new \right)}}-{{L}_{\left( old \right)}}}{{{L}_{\left( old \right)}}}$ and ${{Y}_{o}}=\dfrac{F{{L}_{old}}}{A\left( {{L}_{new}}-{{L}_{old}} \right)}$. Here, F is the force and ${{L}_{\left( old \right)}}$ is the original length of the object and ${{L}_{\left( new \right)}}$ is the new length of an object. A is called the cross-sectional area.

Complete step-by-step answer:
Young’s Modulus: In simple language it is referred to as the modulus of elasticity of any material which can remain unaffected by the changes caused in the length of the material. That is the elasticity of the object remains undamaged even after creating tension in its length by either elongating it or compressing it. To find its numerical form we will consider an example for that. Suppose that there is an object which is of the form of a cube. Let us consider that forces are exerted by elongating its length by its two end points by considering the two forces as ${{F}_{1}}$ and ${{F}_{2}}$ which may or may not be equal. This is shown below.

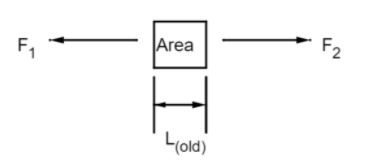
Here, ${{L}_{\left( old \right)}}$ is the original length of the object. As a result of the tension created by the forces the object will change its length from its original position to its new length as ${{L}_{\left( new \right)}}$. This can be seen in the below mentioned diagram.

The stress created here can be found out by the ratio of the force F which is up to an extent which can be stretched without breaking to the cross-sectional area represented as Area or A. This is numerically written as $Stress=\dfrac{F}{A}$. Due to the elongation of the object the strain on the object is calculated as $Strain=\dfrac{{{L}_{\left( new \right)}}-{{L}_{\left( old \right)}}}{{{L}_{\left( old \right)}}}$. Now, the ratio of stress to the strain is known as the Young’s Modulus. We can also numerically form an equation of the Young’s Modulus which can be written as,
$\begin{aligned} & {{Y}_{o}}=\dfrac{Stress}{Strain} \\\ & \Rightarrow {{Y}_{o}}=\dfrac{\dfrac{F}{A}}{\dfrac{{{L}_{\left( new \right)}}-{{L}_{\left( old \right)}}}{{{L}_{\left( old \right)}}}} \\\ & \Rightarrow {{Y}_{o}}=\dfrac{F{{L}_{old}}}{A\left( {{L}_{new}}-{{L}_{old}} \right)} \\\ \end{aligned}$
Now, with the help of the equation of Young’s Modulus we can have the Young’s Modulus of iron as
${{Y}_{\left( iron \right)}}=\dfrac{{{F}_{\left( iron \right)}}{{L}_{old}}}{A\left( {{L}_{new}}-{{L}_{old}} \right)}$ and that of copper as ${{Y}_{\left( copper \right)}}=\dfrac{{{F}_{\left( copper \right)}}{{L}_{old}}}{A\left( {{L}_{new}}-{{L}_{old}} \right)}$. Since, it is given that the two identical wires of iron and copper with their Young’s modulus as a ratio of 3:1 is suspended at same level so, we have that the ratio of ${{Y}_{\left( iron \right)}}=\dfrac{{{F}_{\left( iron \right)}}{{L}_{old}}}{A\left( {{L}_{new}}-{{L}_{old}} \right)}$ to ${{Y}_{\left( copper \right)}}=\dfrac{{{F}_{\left( copper \right)}}{{L}_{old}}}{A\left( {{L}_{new}}-{{L}_{old}} \right)}$ is in the ratio of 3:1 along with the value of ${{L}_{\left( new \right)}}-{{L}_{\left( old \right)}}$ to be equal for both iron and copper. Therefore, we get
$\begin{aligned} & \dfrac{{{Y}_{\left( iron \right)}}}{{{Y}_{\left( copper \right)}}}=\dfrac{3}{1} \\\ & \Rightarrow \dfrac{\dfrac{{{F}_{\left( iron \right)}}{{L}_{old}}}{A\left( {{L}_{new}}-{{L}_{old}} \right)}}{\dfrac{{{F}_{\left( copper \right)}}{{L}_{old}}}{A\left( {{L}_{new}}-{{L}_{old}} \right)}}=\dfrac{3}{1} \\\ & \Rightarrow \dfrac{{{F}_{\left( iron \right)}}}{{{F}_{\left( copper \right)}}}=\dfrac{3}{1} \\\ & \Rightarrow {{F}_{\left( iron \right)}}:{{F}_{\left( copper \right)}}=3:1 \\\ \end{aligned}$
Since, the weight of any object is basically a force of gravity on that particular object which is numerically calculated as $w=mg$ with m as mass and g as a gravitational force on an object. The weight of an object is a force only so, the ratio of their weight will also be 3:1.

So, the correct answer is “Option C”.

Note: The things to be on your finger tips for further questions like this are,
(1) The formula and definition of stress: $Stress=\dfrac{F}{A}$.
(2) The formula and definition of strain: $Strain=\dfrac{{{L}_{\left( new \right)}}-{{L}_{\left( old \right)}}}{{{L}_{\left( old \right)}}}$.
(3) The formula and definition of Young’s Modulus: ${{Y}_{o}}=\dfrac{F{{L}_{old}}}{A\left( {{L}_{new}}-{{L}_{old}} \right)}$.
(4) The fact that the weight of an object is a force only is why the ratio of the weight of iron and copper are the same as 3:1.