Question

The two curves shown in the below figure with $\cosh \left( x \right)$ as green colored and ${{\cosh }^{-1}}\left( x \right)$ as red colored are correctly labeled.

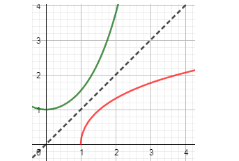
Is the above statement true or false?

Answer 1

Hint : We know that $\cosh \left( x \right)\And {{\cosh }^{-1}}\left( x \right)$ both are hyperbolic functions with $\cosh \left( x \right)=\dfrac{{{e}^{x}}+{{e}^{-x}}}{2}$ and ${{\cosh }^{-1}}\left( x \right)=\ln \left( x+\sqrt{{{x}^{2}}-1} \right)$ . Now, find the minimum value of $\cosh \left( x \right)\And {{\cosh }^{-1}}\left( x \right)$ from the equation that we have just described by putting $x=0$ in these equations and then compare the minimum values from the graph shown in the above problem. If the minimum values of $\cosh \left( x \right)\And {{\cosh }^{-1}}\left( x \right)$ from the equations are matched with the graph given above, then the curves are correctly labeled.

Complete step-by-step answer :
The below graph shown in the above question has two curves marked with red and green colour.

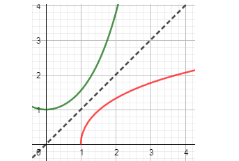
It is given that green color curve corresponds to $\cosh \left( x \right)$ and red color corresponds to ${{\cosh }^{-1}}\left( x \right)$ and we have to show whether the labeling of the curves are correct or not.
We know that $\cosh \left( x \right)\And {{\cosh }^{-1}}\left( x \right)$ are hyperbolic functions. In the below, we are showing the hyperbolic functions in x corresponding to $\cosh \left( x \right)\And {{\cosh }^{-1}}\left( x \right)$ .
The function of $\cosh \left( x \right)$ is equal to:
$\cosh \left( x \right)=\dfrac{{{e}^{x}}+{{e}^{-x}}}{2}$ …………. Eq. (1)
The function of ${{\cosh }^{-1}}\left( x \right)$ is equal to:
${{\cosh }^{-1}}\left( x \right)=\ln \left( x+\sqrt{{{x}^{2}}-1} \right)$ ……….. Eq. (2)
Now, to check whether the curves labeled in the above question are correct or not by finding the minimum values of $\cosh \left( x \right)\And {{\cosh }^{-1}}\left( x \right)$ .
Substituting $x=0$ in eq. (1) we get,
$\begin{aligned} & \cosh \left( 0 \right)=\dfrac{{{e}^{\left( 0 \right)}}+{{e}^{\left( 0 \right)}}}{2} \\\ & \Rightarrow \cosh \left( 0 \right)=\dfrac{1+1}{2} \\\ & \Rightarrow \cosh \left( 0 \right)=\dfrac{2}{2}=1 \\\ \end{aligned}$
Now, at $x=0$ we have got the value of $\cosh \left( x \right)$ as 1 which is the same as given in the above problem.
Hence, the green curve corresponding to $\cosh \left( x \right)$ is correctly labeled.
If we assume that what is given in the question is right i.e. red curve corresponds to ${{\cosh }^{-1}}\left( x \right)$ then the minimum value of this function occurs at $x=1$ and is 0 so let us substitute $x=1$ in eq. (2) to see whether the value of ${{\cosh }^{-1}}\left( x \right)$ is coming 0 or not.
$\begin{aligned} & {{\cosh }^{-1}}\left( x \right)=\ln \left( x+\sqrt{{{x}^{2}}-1} \right) \\\ & \Rightarrow {{\cosh }^{-1}}\left( 1 \right)=\ln \left( 1+\sqrt{{{1}^{2}}-1} \right) \\\ \end{aligned}$
$\begin{aligned} & \Rightarrow {{\cosh }^{-1}}\left( 1 \right)=\ln \left( 1+\sqrt{0} \right) \\\ & \Rightarrow {{\cosh }^{-1}}\left( 1 \right)=\ln \left( 1 \right) \\\ \end{aligned}$
And we know that, the value of $\ln \left( 1 \right)=0$ so the value of the above equation becomes:
${{\cosh }^{-1}}\left( 1 \right)=0$
Hence, we have got the same minimum value of ${{\cosh }^{-1}}\left( x \right)$ which is given in the above problem. Hence, the red curve which is labeled as ${{\cosh }^{-1}}\left( x \right)$ is correct.
From the above, we can say that the above statement is true.

Note : Don’t confuse the functions $\cosh \left( x \right)\And {{\cosh }^{-1}}\left( x \right)$ given in the above problem with $\cos x\And {{\cos }^{-1}}\left( x \right)$ . These two functions are completely different from each other. The functions $\cosh \left( x \right)\And {{\cosh }^{-1}}\left( x \right)$ are hyperbolic functions whereas $\cos x\And {{\cos }^{-1}}\left( x \right)$ are trigonometric functions.
Usually, students ignore the “h” written with cosine and think it might be a typo but it is not so make sure you don’t repeat such mistakes.