Question

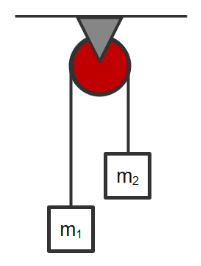
The two blocks in an Atwood machine have masses 2.0 kg and 3.0 kg. Find the work done by gravity during the fourth second after the system is released from rest.(Take $g = 10\,m{s^{ - 1}}$)

Answer 1

in order to solve the question, we will first make the free body diagram of the whole system after then we will make the free body diagram of boxes to find there relation with tension and acceleration using the relation we will find the acceleration after then we will find the distance or the height change in the fourth second after then we will find the work done using the potential energy

Formula used:
${S_{{N^{th}}}} = \dfrac{a}{2}(2n - 1)$
${S_{{N^{th}}}}$ stands for ${n^{th}}$ second
A stand for acceleration
$P.E = mgh$
Where, $M$ stands for mass, $P.E$ stands for potential energy and $H$ stands for change in height.
$F = Ma$
Where, $F$ stands for force.

Complete step by step answer:
In the question we are given the two blocks in an Atwood machine and we have to find the work done by gravity during the fourth second after the system is released from rest.
Mass of boxes:
${M_1} = 3kg$
$\Rightarrow {M_2} = 2kg$

Let the acceleration of the system be “a”. Let the tension of the system be “T”. We will have to find the acceleration in order to proceed in the question for that we will make the free body diagrams

This is the free body diagram of whole system on box of mass 2 kg acceleration and tension both are applied in the upward direction and on box of mass 3 kg acceleration is applied in the downward direction and tension is applied in the upward direction.Now we will make the free body diagrams of the boxes to find the equation between tension and acceleration.

Box 1:

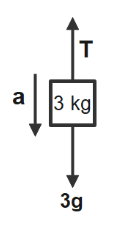
Using the formula of $F = Ma$
$3T - 3g + 3a = 0$ ..(equation 1)

Box 2:

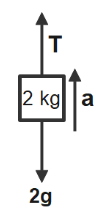
Using the formula of $F = Ma$
$3T - 2g - 2a = 0$ ..(equation 2)
Now solving the equation 1 and 2 for acceleration
Taking the value of tension T from the equation 2
$T{\text{ }} = {\text{ 2}}g{\text{ + 2}}a$
Substituting the value of T in equation 1
$\left( {2g{\text{ + 2}}a} \right){\text{ }} - {\text{ }}3g{\text{ }} + 3a{\text{ }} = {\text{ }}0$
Opening the bracket
$2g + 2a - 3g + 3a = 0$
Value of acceleration
$a = \dfrac{g}{5}m{s^{ - 2}}$
After finding the acceleration we will find the distance travelled in fourth second. To find the distance travelled we use the formula
${S_{{N^{th}}}} = \dfrac{a}{2}(2n - 1)$

Now we will substitute the value of N as 4 and $a = \dfrac{g}{5}m{s^{ - 2}}$
${S_{{4^{th}}}} = \dfrac{{\dfrac{g}{5}}}{2}(2 \times 4 - 1)$
Now taking the 5 with 2 and solving the bracket we get
${S_{{4^{th}}}} = \dfrac{{7g}}{{10}}$
Substituting the value of $g = 10m{s^{ - 1}}$
${S_{{4^{th}}}} = 7m$
Now by using the distance, change in masses we will find the work done that is the potential energy as the block moves at different heights.
Change in mass: 3kg-2kg=1kg
Potential energy formula:$P.E = mgh$
Substituting the values
$P.E = 1 \times 10 \times 7$
$\therefore P.E = 7\,J$

Hence the work done is 70 J.

Note: Many of the students will make the mistake that kinetic energy is not taken in consideration but this is because boxes are moved at a very slow speed which makes kinetic energy negligible and people may mistake by taking fourth second and four second as they have different formula to calculate and one means till four second and other means in the fourth second.