Question

The triangle OAB is a right angled triangle where points O, A and B are (0,0), $(\cos \theta ,\sin \theta )$ and ( $\cos \phi ,\sin \phi$ ) respectively. Then the relation between $\theta$ and $\phi$ is given by:

& (\text{a})\text{ }\sin \left( \dfrac{\theta -\phi }{2} \right)=\dfrac{1}{\sqrt{2}} \\\ & (b)\text{ }cos\left( \dfrac{\theta -\phi }{2} \right)=\dfrac{1}{\sqrt{2}} \\\ & (c)\text{ }cos\left( \dfrac{\theta -\phi }{2} \right)=-\dfrac{1}{\sqrt{2}} \\\ & (d)\text{ }sin\left( \dfrac{\theta -\phi }{2} \right)=-\dfrac{1}{\sqrt{2}} \\\ \end{aligned}$$

Answer 1

- Hint: The hint here is that we will verify the Pythagoras theorem in the given triangle. We will get a condition in terms of ፀ and φ that we need to solve and in the end we will get answer.

Complete step-by-step solution -

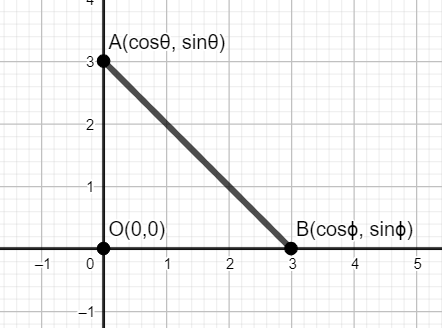
Let us now begin with the solution.
We know distance between two points $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ is given by the formula,
$\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$
Now let us find the distance OA using the distance formula given above,

& =\sqrt{{{\left( {{x}_{O}}-{{x}_{A}} \right)}^{2}}+{{\left( {{y}_{O}}-{{y}_{A}} \right)}^{2}}} \\\ & =\sqrt{{{\left( 0-\cos \theta \right)}^{2}}+{{\left( 0-\sin \theta \right)}^{2}}} \\\ & =\sqrt{{{\left( -\cos \theta \right)}^{2}}+{{\left( -\sin \theta \right)}^{2}}} \\\ & =\sqrt{{{\cos }^{2}}\theta +{{\sin }^{2}}\theta } \\\ \end{aligned}$$ =1 (since $${{\cos }^{2}}\theta +{{\sin }^{2}}\theta $$ = 1) Thus OA = 1 Similarly let us find OB $$\begin{aligned} & =\sqrt{{{\left( {{x}_{O}}-{{x}_{B}} \right)}^{2}}+{{\left( {{y}_{O}}-{{y}_{B}} \right)}^{2}}} \\\ & =\sqrt{{{\left( 0-\cos \phi \right)}^{2}}+{{\left( 0-\sin \phi \right)}^{2}}} \\\ & =\sqrt{{{\left( -\cos \phi \right)}^{2}}+{{\left( -\sin \phi \right)}^{2}}} \\\ & =\sqrt{{{\cos }^{2}}\phi +{{\sin }^{2}}\phi } \\\ \end{aligned}$$ =1 (since $${{\cos }^{2}}\phi +{{\sin }^{2}}\phi $$ = 1) Thus OB = 1 Consider the points $A\left( \cos \theta ,\sin \theta \right),B\left( \cos \phi ,\sin \phi \right)$. Here, $\left( {{x}_{A}}=\cos \theta ,{{x}_{B}}\sin \theta \right),\left( {{y}_{A}}=\cos \phi ,{{y}_{B}}=\sin \phi \right)$ Now let us find the distance between AB using the above values, we get $$\begin{aligned} & =\sqrt{{{\left( {{x}_{A}}-{{x}_{B}} \right)}^{2}}+{{\left( {{y}_{A}}-{{y}_{B}} \right)}^{2}}} \\\ & =\sqrt{{{\left( \cos \theta -\cos \phi \right)}^{2}}+{{\left( sin\theta -\sin \phi \right)}^{2}}} \\\ & =\sqrt{\left( {{\cos }^{2}}\theta -2\cos \theta \cos \phi +{{\cos }^{2}}\phi +{{\sin }^{2}}\theta -2\sin \theta \sin \phi +{{\sin }^{2}}\phi \right)} \\\ \end{aligned}$$ Now $${{\cos }^{2}}\theta +{{\sin }^{2}}\theta $$ = 1 and $${{\cos }^{2}}\phi +{{\sin }^{2}}\phi $$ = 1. Therefore, $$\begin{aligned} & =\sqrt{\left( 2-2\cos \theta \cos \phi -2\sin \theta \sin \phi \right)} \\\ & =\sqrt{2-2\left( \cos \theta \cos \phi +\sin \theta \sin \phi \right)} \\\ \end{aligned}$$ Now since $$\left( \cos \theta \cos \phi +\sin \theta \sin \phi \right)$$ = $$\cos \left( \theta -\phi \right)$$ we get, $$=\sqrt{2\left( 1-\cos \left( \theta -\phi \right) \right)}$$ Thus AB = $$\sqrt{2\left( 1-\cos \left( \theta -\phi \right) \right)}$$ Now let us apply Pythagoa's theorem on sides OA, OB and AB. Doing so we get, $$\begin{aligned} & O{{A}^{2}}+O{{B}^{2}}=A{{B}^{2}} \\\ & {{1}^{2}}+{{1}^{2}}={{\left( \sqrt{2\left( 1-\cos \left( \theta -\phi \right) \right)} \right)}^{2}} \\\ & \Rightarrow 2=2\left( 1-\cos \left( \theta -\phi \right) \right) \\\ & \Rightarrow 1=\left( 1-\cos \left( \theta -\phi \right) \right) \\\ \end{aligned}$$ Cancelling one on both the sides we get, $$\cos \left( \theta -\phi \right)=0$$ Thus $$\left( \theta -\phi \right)=(n+1)\dfrac{\pi }{2}$$ This is because cosine function attains 0 value only at odd multiples of $$\dfrac{\pi }{2}$$. Now dividing by 2 on both the sides, we get, $$\dfrac{\left( \theta -\phi \right)}{2}=\left( n+1 \right)\dfrac{\pi }{4}$$ Now apply the cosine function on both sides. Doing so we get, $$\begin{aligned} & \cos \left( \dfrac{\left( \theta -\phi \right)}{2} \right)=\cos \left( \left( n+1 \right)\dfrac{\pi }{4} \right) \\\ & \cos \left( \dfrac{\left( \theta -\phi \right)}{2} \right)=\pm \dfrac{1}{\sqrt{2}} \\\ \end{aligned}$$ Since odd multiples of $$\dfrac{\pi }{4}$$ result in $$\pm \dfrac{1}{\sqrt{2}}$$ when we apply the cos function. Now we apply sine function on both sides. Doing so we get, $$\begin{aligned} & sin\left( \dfrac{\left( \theta -\phi \right)}{2} \right)=sin\left( \left( n+1 \right)\dfrac{\pi }{4} \right) \\\ & sin\left( \dfrac{\left( \theta -\phi \right)}{2} \right)=\pm \dfrac{1}{\sqrt{2}} \\\ \end{aligned}$$ Since odd multiples of $$\dfrac{\pi }{4}$$ result in $$\pm \dfrac{1}{\sqrt{2}}$$ when we apply sin function. Now as we can see we have our answers. The two answers we got satisfy all the options given in the question. Thus the correct options are option(a), option(b), option(c) and option(d). Note: You should be very careful while writing the term $$\left( \dfrac{\left( \theta -\phi \right)}{2} \right)$$ in terms of angles. The angles should be in the form of a multiple of some specific angle. This is the general solution of a trigonometric function. If you write only one value/principal value, we get only 2 answers which though correct can result in partial marking and thus deduction.