Question

The triangle joining the points P (2, 7), Q (4, -1), R (-2, 6) is:
A. an equilateral triangle
B. a right angled triangle
C. an isosceles triangle
D. a scalene triangle

Answer 1

Hint : Triangles are of different types depending upon the angles they make. Though the sum of all the three angles in any triangle is 180°. We have been given three non-collinear points which form a triangle.
Formula used: Distance formula:
$D = \sqrt {{{(x - {x_1})}^2} + {{(y - {y_1})}^2}}$

Complete step-by-step answer :
Therefore let us plot these points and observe if all the sides of the triangle are equal then the triangle formed will be an equilateral triangle. If only two of the sides are equal in magnitude then the formed triangle is an isosceles triangle. If none of the sides are equal to each other then the triangle is a scalene triangle. Also if the sides of the triangle follows the formula given below,
${b^2} + {p^2} = {(hyp)^2}$
Where b is the base of the triangle, p is the perpendicular and (hyp) is the hypotenuse of the triangle which is the longest side facing the angle of 90°, is called a right angled triangle.
The length of the sides can be found out by the distance formula which will find the distance between any two given points.

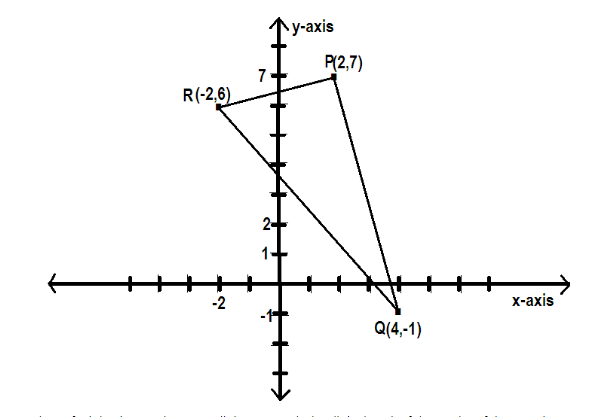
Now let us find the distance between all the points which will the length of three sides of the triangle,
Length of the side PQ is
$\Rightarrow PQ = \sqrt {{{(4 - 2)}^2} + {{(( - 1) - 7)}^2}} \\\ \Rightarrow PQ = \sqrt {{2^2} + {{( - 8)}^2}} = \sqrt {4 + 64} \\\ \Rightarrow PQ = \sqrt {68} \;$
Length of the side QR is
$\Rightarrow QR = \sqrt {{{( - 2 - 4)}^2} + {{( - 6 - 1)}^2}} \\\ \Rightarrow QR = \sqrt {{{( - 6)}^2} + {{( - 7)}^2}} = \sqrt {36 + 49} \\\ \Rightarrow QR = \sqrt {85} \;$
Length of the side PR is
$\Rightarrow PR = \sqrt {{{\left( { - 2 - 2} \right)}^2} + {{\left( {6 - 7} \right)}^2}} \\\ \Rightarrow PR = \sqrt {{{( - 4)}^2} + {{( - 1)}^2}} \\\ \Rightarrow PR = \sqrt {16 + 1} = \sqrt {17} \;$
Since the longest side is QR it must be the hypotenuse of the triangle, PQ the base and PR the perpendicular. Hence substituting the values in the formula to check whether this triangle is a right angle triangle.
$\Rightarrow {\left( {PQ} \right)^2} + {\left( {PR} \right)^2} = {\left( {QR} \right)^2} \\\ \Rightarrow {\left( {\sqrt {68} } \right)^2} + {\left( {\sqrt {17} } \right)^2} = {\left( {\sqrt {85} } \right)^2} \;$
Square root cancels the square,
$\Rightarrow 68 + 17 = 85 \\\ \Rightarrow 85 = 85 \;$
Hence proved. Therefore the correct option is B.
So, the correct answer is “Option B”.

Note : The formula ${b^2} + {p^2} = {(hyp)^2}$ is called the Pythagoras theorem. It states true for every right angle triangle where hypotenuse is the side facing the angle of 90° and is thus the longest side.