Question

The triangle formed by the three points whose position vectors are $2i+4j-k$, $4i+5j+k$ and $3i+6j-3k$, is
(A) An equilateral triangle
(B) A right-angled triangle but not isosceles
(C) An isosceles triangle but not right-angled triangle
(D) A right-angled isosceles triangle
(E) A scalene triangle

Answer 1

We solve this question by first considering the position vectors and then we assume the points as A, B and C. Then we continue by finding the sides of the triangle from the given position vectors of the points. Then we find the lengths of the sides and see if any of them are equal. Then we verify the Pythagoras theorem, in a right-angled triangle square of hypotenuse is equal to sum of squares of other two sides. By the obtained results we can say the nature of the triangle and mark the correct option.

Complete step by step answer:
We are given that the position vectors of the three points of the triangle are $2i+4j-k$, $4i+5j+k$ and $3i+6j-3k$.
Let us assume the points are $A,2i+4j-k$, $B,4i+5j+k$ and $C,3i+6j-3k$.
So, the triangle formed by them is triangle ABC.

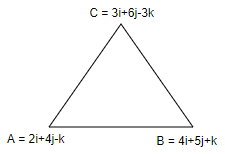
Now let us find the sides of the triangle ABC.
First, let us find the side AB.
$\begin{aligned} & \Rightarrow \overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA} \\\ & \Rightarrow \overrightarrow{AB}=\left( 4i+5j+k \right)-\left( 2i+4j-k \right) \\\ & \Rightarrow \overrightarrow{AB}=2i+j+2k \\\ \end{aligned}$
Now, let us find the side BC.
$\begin{aligned} & \Rightarrow \overrightarrow{BC}=\overrightarrow{OC}-\overrightarrow{OB} \\\ & \Rightarrow \overrightarrow{BC}=\left( 3i+6j-3k \right)-\left( 4i+5j+k \right) \\\ & \Rightarrow \overrightarrow{BC}=-i+j-4k \\\ \end{aligned}$
Now, let us find the side CA.
$\begin{aligned} & \Rightarrow \overrightarrow{CA}=\overrightarrow{OA}-\overrightarrow{OC} \\\ & \Rightarrow \overrightarrow{CA}=\left( 2i+4j-k \right)-\left( 3i+6j-3k \right) \\\ & \Rightarrow \overrightarrow{CA}=-i-2j+2k \\\ \end{aligned}$
So, we get the sides of the triangle ABC as, $\overrightarrow{AB}=2i+j+2k$, $\overrightarrow{BC}=-i+j-4k$ and $\overrightarrow{CA}=-i-2j+2k$.
Now let us find the lengths of sides.
We get the lengths of side AB as,
$\begin{aligned} & \Rightarrow \left| \overrightarrow{AB} \right|=\sqrt{{{2}^{2}}+{{1}^{2}}+{{2}^{2}}} \\\ & \Rightarrow \left| \overrightarrow{AB} \right|=\sqrt{4+1+4} \\\ & \Rightarrow \left| \overrightarrow{AB} \right|=\sqrt{9} \\\ & \Rightarrow \left| \overrightarrow{AB} \right|=3 \\\ \end{aligned}$
We get the lengths of side BC as,
$\begin{aligned} & \Rightarrow \left| \overrightarrow{BC} \right|=\sqrt{{{\left( -1 \right)}^{2}}+{{1}^{2}}+{{\left( -4 \right)}^{2}}} \\\ & \Rightarrow \left| \overrightarrow{BC} \right|=\sqrt{1+1+16} \\\ & \Rightarrow \left| \overrightarrow{BC} \right|=\sqrt{18} \\\ & \Rightarrow \left| \overrightarrow{BC} \right|=3\sqrt{2} \\\ \end{aligned}$
We get the lengths of side CA as,
$\begin{aligned} & \Rightarrow \left| \overrightarrow{CA} \right|=\sqrt{{{\left( -1 \right)}^{2}}+{{\left( -2 \right)}^{2}}+{{2}^{2}}} \\\ & \Rightarrow \left| \overrightarrow{CA} \right|=\sqrt{1+4+4} \\\ & \Rightarrow \left| \overrightarrow{CA} \right|=\sqrt{9} \\\ & \Rightarrow \left| \overrightarrow{CA} \right|=3 \\\ \end{aligned}$
So, we can see that lengths of sides AB and CA are equal. So, it is an isosceles triangle.
Now let us consider the Pythagoras theorem. In a right-angled triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.
Here we can see that,
$\begin{aligned} & \Rightarrow B{{C}^{2}}={{\left( 3\sqrt{2} \right)}^{2}}=18 \\\ & \Rightarrow B{{C}^{2}}=9+9 \\\ & \Rightarrow B{{C}^{2}}={{3}^{2}}+{{3}^{2}} \\\ & \Rightarrow B{{C}^{2}}=A{{B}^{2}}+C{{A}^{2}} \\\ \end{aligned}$
So, ABC is a right-angled triangle at A.
So, the triangle ABC is a right-angled isosceles triangle.

So, the correct answer is “Option D”.

Note: The common mistake one makes while solving this question is one might stop the question after finding that it is isosceles triangle and not check whether it is right angled triangle or not and mark the answer as option C. So, we need to check all the possibilities.