Question

The transverse axis of a hyperbola is of length 2a and a vertex divides the segment of the axis between the centre and the corresponding focus in the ratio 2:1. The equation of the hyperbola is

$$\left( a \right)4{x^2} - 5{y^2} = 4{a^2} \\\ \left( b \right)4{x^2} - 5{y^2} = 5{a^2} \\\ \left( c \right)5{x^2} - 4{y^2} = 4{a^2} \\\ \left( d \right)5{x^2} - 4{y^2} = 5{a^2} \\\$$

Answer 1

Hint-In this question, we use the property of the hyperbola. We know the eccentricity of hyperbola $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$ is $e = \dfrac{{\sqrt {{a^2} + {b^2}} }}{a}$ where $a$ is length of semi transverse axis and $b$ is length of semi conjugate axis. To find eccentricity(e) use section formula and find x coordinate.

Complete step-by-step answer:
Given, length of transverse axis is 2a so the length of semi transverse axis is a.
Let equation of hyperbola is $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1...............\left( 1 \right)$
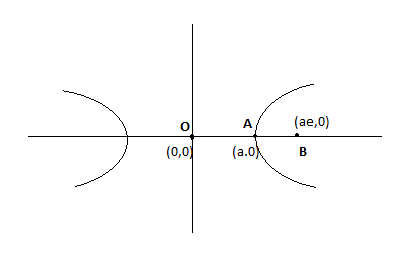
From figure, coordinate of vertex A(a, 0), Focus B(ae, 0) and centre O(0, 0).
Now, vertex A (a, 0) divides the line joining between focus B (ae, 0) and centre O (0, 0) in the ratio 2:1.
We have to apply section formula,
$x = \dfrac{{{m_1}{x_2} + {m_2}{x_1}}}{{{m_1} + {m_2}}}{\text{ and y}} = \dfrac{{{m_1}{y_2} + {m_2}{y_1}}}{{{m_1} + {m_2}}}{\text{ }}$ where $\left( {x,y} \right)$ divide the line segment joining between the points $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ in the ratio ${m_1}:{m_2}$ .
$\Rightarrow a = \dfrac{{2ae + 1 \times 0}}{{2 + 1}} \\\ \Rightarrow a = \dfrac{{2ae}}{3} \\\ \Rightarrow e = \dfrac{3}{2} \\\$
Now, use $e = \dfrac{{\sqrt {{a^2} + {b^2}} }}{a}$
$\Rightarrow \dfrac{3}{2} = \dfrac{{\sqrt {{a^2} + {b^2}} }}{a}$
Squaring both sides,
$\Rightarrow \dfrac{9}{4} = \dfrac{{{a^2} + {b^2}}}{{{a^2}}}$
Cross multiplication,
$\Rightarrow 9{a^2} = 4\left( {{a^2} + {b^2}} \right) \\\ \Rightarrow 9{a^2} = 4{a^2} + 4{b^2} \\\ \Rightarrow 5{a^2} = 4{b^2} \\\ \Rightarrow {b^2} = \dfrac{{5{a^2}}}{4} \\\$
Put the value of b2 in (1) equation,
$\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{\dfrac{{5{a^2}}}{4}}} = 1 \\\ \Rightarrow \dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{4{y^2}}}{{5{a^2}}} = 1 \\\ \Rightarrow 5{x^2} - 4{y^2} = 5{a^2} \\\$
Hence, the equation of hyperbola is $5{x^2} - 4{y^2} = 5{a^2}$
So, the correct option is (d).
Note- In such types of problems we should remember the coordinates of vertex, Focus and centre of hyperbola and then find the value of eccentricity with the help of these coordinates and section formula. Then after using the eccentricity formula we can easily make a relation between a and b.