Question

The top of a hill observed from the top and bottom of a building of height h is at angles of elevation p and q respectively. The height of the hill.

$$A.{\text{ }}\dfrac{{h\cot q}}{{\cot a - \cot q}} \\\ B.{\text{ }}\dfrac{{h\cot p}}{{\cot p - \cot q}} \\\ C.{\text{ }}\dfrac{{h\tan p}}{{\tan p - \tan q}} \\\ D.{\text{ }}None{\text{ }}of{\text{ }}these \\\$$

Answer 1

Hint: This problem is based on the application of trigonometry. Start with assuming the height of the hill and the distance between the hill and the building as different variables H and x. Analyse the situation with a diagram and use trigonometric identity $\tan \theta = \dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}}$ for two different triangles. Finally compare both the results and simplify it further to find the height of the hill.

Complete step-by-step answer:
Let the height of the hill is equal to H.
And the distance between the base of the building and the hill is equal to x.

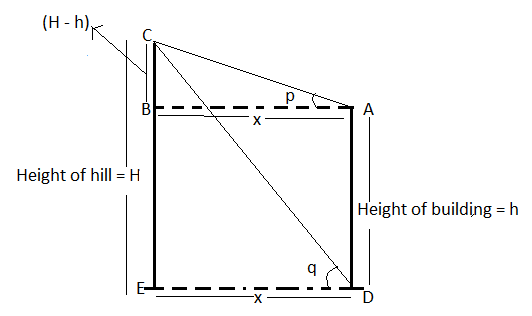
Now as we can see from the above figure that the length of BC is equal to (H – h) and the distance between building and hill (i.e. BA and ED) is equal to x.
So, now according trigonometric formula $\tan \theta = \dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}}$
$\tan p = \dfrac{{BC}}{{BA}} = \dfrac{{H - h}}{x}$ (1)
$\tan q = \dfrac{{CE}}{{ED}} = \dfrac{H}{x}$ (2)
Now solving equation 2 to find the value of x. We get,
$x = \dfrac{H}{{\tan q}}$
Now putting the value of x in equation 1. We get,
$\tan p = \dfrac{{\left( {H - h} \right)\tan q}}{H}$
Now cross multiplying the above equation. We get,

$$H\tan p = H\tan q - h\tan q \\\ H\tan q - H\tan p = h\tan q \\\$$

$H = \dfrac{{h\tan q}}{{\tan q - \tan p}}$ (3)
Now as we know that $\tan \theta = \dfrac{1}{{\cot \theta }}$
So, now replacing $\tan p$ and $\tan q$ in equation 3 with $\cot p$ and $\cot q$. We get,
$H = \dfrac{{\dfrac{h}{{\cot q}}}}{{\dfrac{1}{{\cot q}} - \dfrac{1}{{\cot p}}}}$
Now taking LCM in the denominator of RHS of the above equation and then solving. We get,
$H = \dfrac{{\dfrac{h}{{\cot q}}}}{{\dfrac{{\cot p - \cot q}}{{\left( {\cot q} \right)\left( {\cot p} \right)}}}} = \dfrac{{h\cot p}}{{\cot p - \cot q}}$
So, the height of the hill must be equal to $\dfrac{{h\cot p}}{{\cot p - \cot q}}$
Hence, the correct option will be B.

Note:- Whenever we come up this type of problem then first, we had to find equations for $\tan p$ and $\tan q$ and then using substitution method we can find the value of x (distance between hill and building) using one equation and then put that value of x in other equation to find the value of H. Now if the height of hill is in terms of $\tan p$ and $\tan q$ then we can change $\tan p$ to $\cot p$ and $\tan q$ to $\cot q$ using formula $\tan \theta = \dfrac{1}{{\cot \theta }}$. This will be the easiest and efficient way to find the solution of the problem.