Question

The time taken by the boat to cross the river:

Answer 1

In this question we will use the relation between the net velocity and the angle made by the boat. This will give us the required result. Also, we will discuss the basics of time and time of flight. Also, we will see the basic difference between speed and velocity for our better understanding.

Formula used:
${V_{net}} = 2v\cos \theta$
$\dfrac{{d\theta }}{{dt}} = \dfrac{{{V_{net}}}}{{2\omega }}$

Complete step-by-step answer:
Let us assume that at any time t, the boat is at point B, and then we have the equation as:

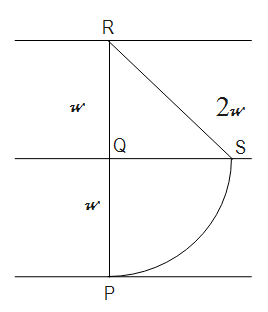
${V_{net}} = 2v\cos \theta$
$\dfrac{{d\theta }}{{dt}} = \dfrac{{{V_{net}}}}{{2\omega }} = \dfrac{{v\cos \theta }}{\omega }$
$\Rightarrow \dfrac{\omega }{v}\sec \theta d\theta = dt$
Now, by integrating both sides with respect to time t, we get:
$\int_0^t {dt} = \dfrac{\omega }{v}\int_0^{{{60}^ \circ }} {\sec \theta d\theta }$
By solving the above equation:
$t = \dfrac{\omega }{v}\left[ {\ln (sec\theta + tan\theta )} \right]_0^{{{60}^ \circ }}$
$\therefore t = \dfrac{{1.317\omega }}{v}$
Therefore, we get the required result, which gives us the time taken by the boat to cross the given river.

Additional Information:
As we know, time is a very important measure. The S.I unit of time is second. Time is given by the ratio of distance travelled by an object and the velocity or speed of the object.
We already know the basic difference of speed and velocity i.e., speed is the measure of how fast an object can travel, whereas velocity tells us the direction of this speed. Speed is a scalar quantity that means it has only magnitude, whereas velocity is a vector quantity that means it has both magnitude and direction. The S.I unit of velocity is meter per second (m/sec).
Also, time of flight can be defined as the measurement of the time taken by an object or particle (be it acoustic, electromagnetic) to travel a particular distance through a medium.

Note: Here, it is important to remember that time of flight can be measured for waves as well. We know that the S.I unit of speed is m/sec but the speedometer shows the value in km/h. Therefore, the question can be directly solved by having an idea of the unit of speed.