Question

The time taken by a particle performing S.H.M. to pass from point A to B where its velocities are the same is $2$ seconds. After another $2$ seconds, it returns to B. Determine the time period of oscillation is (in seconds).
A. $2$
B. $4$
C. $6$
D. $8$

Answer 1

Concept of simple harmonic motion and time period in SHM is to be used to find the time period here. Also as we know that time period is time taken to complete one rotation and to return to the same position after one complete rotation.

Formula used:
$x = A{\text{ sin }}\omega {\text{t}}$
Where x is the displacement at time t
A is the amplitude
And w is the angular frequency

Complete step by step answer:
SHM – A particle is in SHM if it moves to and fro about the mean position under the action of restoring force proportional to its displacement from mean position and is always directed towards the mean position i.e. $F \propto x{\text{ }} \Rightarrow {\text{F}} = - Kx$
Equation of SHM
In SHM, Force, F is related to displacement x as
$F = - Kx$…….. (i)
The negative sign shows force and $x$ are in opposite direction
By Newton’s second law, Force is the product of mass (m) and acceleration (a). So, we can write force as
$F = ma = \dfrac{{m{d^2}x}}{{dt}}$…….. (ii)
From (i) and (ii)
$\dfrac{{m{d^2}x}}{{d{t^2}}} = - Kx$
$\dfrac{{{d^2}x}}{{d{t^2}}} = \dfrac{{ - K}}{m}x$
Let $\dfrac{K}{m} = {\omega ^2},{\text{ }}\omega \to$ angular frequency and k is a constant of proportionality.
So, $\dfrac{{{d^2}x}}{{d{t^2}}} = - {\omega ^2}x$
$\dfrac{{{d^2}x}}{{d{t^2}}} + {\omega ^2}x = 0$
Which the differential equation of SHM
The solution of such equation is given by
$x = A\sin \omega t$….. (iii)
Where $x$ is the displacement from mean position at time $t$
$A$ is amplitude
$\omega$ is angular frequency
And $\omega = \dfrac{{2\pi }}{T}$ where $T$ is the time period of SHM.
Now according to question

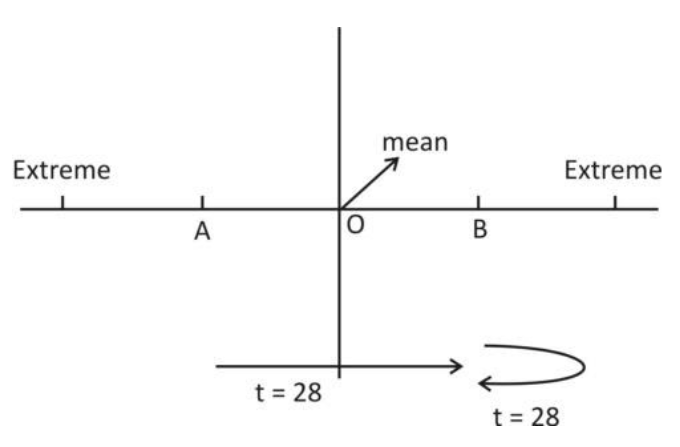
We have the above figure.
Now, the time period is the time taken to complete one complete oscillation.
Time taken for A to B $= 2\sec$
Time taken from B to extreme
And back to B $= 2\sec$
Time taken from A to extreme and back to A $=$ time taken from b to extreme to back to B
Similarly, time taken for A to B $=$ time taken from B to A
Time period $=$ Time taken (A to B) $+$ Time taken (B$\to$extreme$\to$B) $+$ Time taken (B to A) $+$ time taken (A$\to$extreme$\to$A)
Time period$= 2 + 2 + 2 + 2 = 8\sec$.

So, the correct answer is “Option D”.

Note:
One complete oscillation includes passing from one point twice and the time period is the time taken to complete one complete oscillation.