Question

The time constant of a circuit is $10{\text{ }}\sec$, when a resistance of $10{\text{ }}\Omega$ is connected in series in a previous circuit then time constant becomes ${\text{2}}$ second, then the self-inductance of the circuit is:
A. $2.5{\text{ }}H$
B. $5{\text{ }}H$
C. ${\text{15 }}H$
D. ${\text{25 }}H$

Answer 1

Here it is given that the time constant of a circuit is $10{\text{ }}\sec$ when an inductor and a resistor are connected in a series. The time constant changes when another resistance is connected with it in series. Hence, we have to formulate equations using the relation between time constant, resistance and inductance. Then by comparing the equations we will find the answer.

Complete step by step answer:
It is given in the question that when a resistance and inductor are connected in series then the time constant is $10{\text{ }}\sec$.
Let the resistance of the circuit be $R$ and the inductance of the circuit be $L$

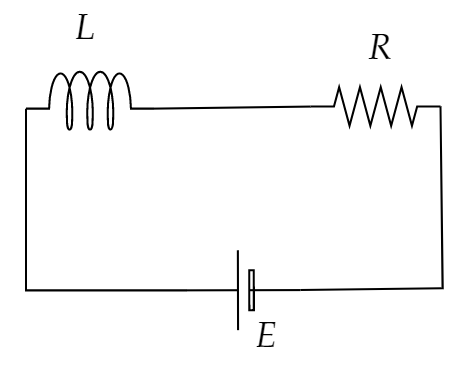
The relation between time constant $\tau = 2{\text{ }}\sec$, resistance $R$ and inductance $L$ is,
$\tau = \dfrac{L}{R} - - - - - \left( 1 \right)$
Substituting the value of $\tau$ we get,
$10 = \dfrac{L}{R}$
$\Rightarrow L = 10R - - - - - \left( 2 \right)$
Again, it is given that a new resistance of $10{\text{ }}\Omega$ is connected in series with the circuit,
Thus, the new resistance of the circuit $R' = (10 + R){\text{ }}\Omega$
The new time constant is given as $\tau ' = 2{\text{ }}\sec$
The inductance remains the same $L$.

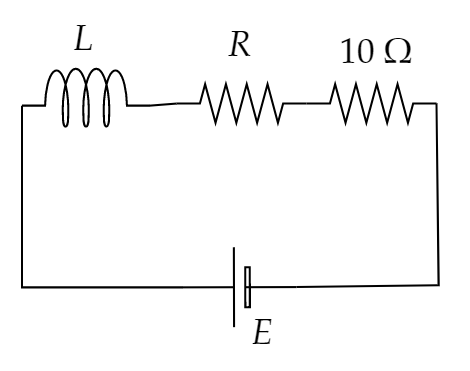
Thus, from equation $\left( 1 \right)$ we get,
$2 = \dfrac{L}{{10 + R}}$
$\Rightarrow L = 20 + 2R - - - - - \left( 3 \right)$
Comparing equation $\left( 2 \right)$ and $\left( 3 \right)$ we get,
$10R = 20 + 2R$
$\Rightarrow R = 2.5{\text{ }}\Omega$
Substituting the value of $R$ in equation $\left( 2 \right)$ we get,
$L = 2.5 \times 10 = 25{\text{ }}H$
Thus, the self-inductance of the coil is $25{\text{ }}H$.
The correct option is D. ${\text{25 }}H$.

Note: It must be noted that in this case self-inductance is developed as there is only one inductor. Self-inductance of a circuit is defined as the property of the coil by which an induced emf is developed in the coil due to the change in current flowing through it.