Question

The three vertices of a parallelogram are (3, 4), (3, 8) and (9, 8). Find the fourth vertex.

Answer 1

Hint: Assume the coordinate of the fourth vertex of parallelogram ABCD to be (x,y). We know that the diagonal of a parallelogram bisects each other. Since ABCD is a parallelogram, the diagonals must bisect each other. We know that the midpoint(x,y) of A $({{x}_{1}},{{y}_{1}})$ and B $({{x}_{2}},{{y}_{2}})$ is $x=\dfrac{{{x}_{1}}+{{x}_{2}}}{2}$ , $y=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}$ . Using the midpoint formula, find the coordinate of the midpoint of the diagonal BD. Similarly, find the midpoint of the coordinate of the diagonal AC. Since the diagonals meet at a point O. So, the midpoint of the diagonal AC and the diagonal BD must coincide. Now, solve it further and get the values of x and y.

Complete step-by-step answer:

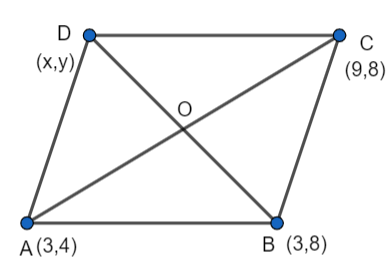
Let the coordinate of the fourth vertex D be (x,y).
We know that the diagonals of a parallelogram bisect each other. Since ABCD is a parallelogram, the diagonals must bisect each other.
For diagonal AC, O is its midpoint.
We know the formula that the midpoint(x,y) of A $({{x}_{1}},{{y}_{1}})$ and B $({{x}_{2}},{{y}_{2}})$ is $x=\dfrac{{{x}_{1}}+{{x}_{2}}}{2}$ , $y=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}$ .
As O is the midpoint of the diagonal AC, we can find its coordinates using the midpoint formula.
We have, A = (3,4) and C = (9,8),
O = $\left( \dfrac{3+9}{2},\dfrac{4+8}{2} \right)$ = $\left( 6,6 \right)$ ……………………….(1)
As O is the midpoint of the diagonal BD, we can find its coordinates using the midpoint formula.
We have, B = (3,8) and D = (x,y),
O = $\left( \dfrac{3+x}{2},\dfrac{8+y}{2} \right)$ …………………….(2)
Comparing equation (1) and equation (2), we get
$6=\dfrac{3+x}{2}$ ………………….(3)
$6=\dfrac{8+y}{2}$ ………………….(4)
Solving equation (3), we get

& 6=\dfrac{3+x}{2} \\\ & \Rightarrow 12=3+x \\\ & \Rightarrow 9=x \\\ \end{aligned}$$ Solving equation (4), we get $$\begin{aligned} & 6=\dfrac{8+y}{2} \\\ & \Rightarrow 12=8+y \\\ & \Rightarrow 4=y \\\ \end{aligned}$$ The values of x and y are 4 and 9 respectively. So, D = (9,4). Hence, the fourth vertex is (9,4). Note: We can also solve this question using the distance formula.  Let the fourth vertex of the parallelogram be (x,y). We know that the opposite sides of a parallelogram are equal to each other. So, AB = CD and BC = AD. AB = $$\sqrt{{{(3-3)}^{2}}+{{(4-8)}^{2}}}=4$$ …………………(1) BC = $$\sqrt{{{(3-9)}^{2}}+{{(8-8)}^{2}}}=6$$ ……………………..(2) CD = $$\sqrt{{{(9-x)}^{2}}+{{(8-y)}^{2}}}=\sqrt{{{x}^{2}}+{{y}^{2}}-18x-16y+145}$$ ………………………(3) AD = $$\sqrt{{{(3-x)}^{2}}+{{(4-y)}^{2}}}=\sqrt{{{x}^{2}}+{{y}^{2}}-6x-8y+25}$$ ……………………..(4) From equation (1) and equation (3), we get $$A{{B}^{2}}=C{{D}^{2}}$$ $${{4}^{2}}={{x}^{2}}+{{y}^{2}}-18x-16y+145$$ …………………..(5) From equation (2) and equation (4), we get $$B{{C}^{2}}=A{{D}^{2}}$$ $${{6}^{2}}={{x}^{2}}+{{y}^{2}}-6x-8y+25$$ …………………..(6) We have two equations and two variables. On solving equation (5) and equation (6), we get x=9 and y=4. Hence, the fourth vertex is (9,4).