Question

The three vertices of a parallelogram A(3,-4), B(-1,-3), and C(-6,2). Find the coordinate of vertex D and find the area of ABCD.

Answer 1

Using the property of parallelogram i.e. diagonal of a parallelogram bisect each other we will find the coordinate of the intersection of diagonal using mid-point formula i.e.
If (l,m) is the mid-point of (x,y) and (p,q) then
then, $l = \dfrac{{x + p}}{2}$
and $m = \dfrac{{y + q}}{2}$
Further, we will find the coordinate of D having the same procedure.
If in triangle PQR, $P({x_1},{y_1})$,$Q({x_2},{y_2})$ and $R({x_3},{y_3})$
Then the area of triangle PQR$= \dfrac{1}{2}\left[ {{x_1}({y_2} - {y_3}) + {x_2}({y_3} - {y_1}) + {x_3}({y_1} - {y_2})} \right]$

Complete step-by-step answer:
Given data: A(3,-4), B(-1,-3), and C(-6,2)

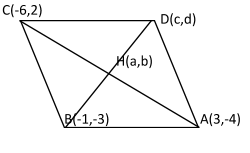
let the coordinate of D be (c,d) and H, the intersection point of diagonal be
(a,b)
We know that H is the mid-point of AC
Therefore, using the mid-point formula on AC,
i.e. $a = \dfrac{{ - 6 + 3}}{2}$
$\Rightarrow a = \dfrac{{ - 3}}{2}$
And, $b = \dfrac{{2 - 4}}{2}$
$\therefore b = - 1\;$
Therefore, the coordinate of $H(\dfrac{{ - 3}}{2}, - 1)$
Since H is also the mid-point of BD, using the mid-point formula we get,
i.e. $a = \dfrac{{ - 1 + c}}{2}$
on substituting the value of a,
i.e. $\dfrac{{ - 3}}{2}\; = \;\dfrac{{ - 1 + c}}{2}{\text{ }}\;{\text{ }}$
$\Rightarrow \; - 3 = - 1 + c\;$
$\therefore c = - 2\;$
And, $b = \dfrac{{3 + d}}{2}$
on substituting the value of b, we get
$\Rightarrow - 1\; = \dfrac{{ - 3 + d}}{2}$
$\Rightarrow - 2\; = - 3 + d$
$\therefore d = 1$
Therefore, the coordinate of $D( - 2,1)$
Since the diagonal of a parallelogram divides the parallelogram into two equal parts. We can say that area of parallelogram ABCD is twice the area of triangle ABC
Therefore, the area of triangle ABC$= \dfrac{1}{2}\left[ {{x_1}({y_2} - {y_3}) + {x_2}({y_3} - {y_1}) + {x_3}({y_1} - {y_2})} \right]$
Substituting the value of vertices of triangle ABC.
$= \dfrac{1}{2}\left[ {3( - 3 - 2) - 1(2 + 4) - 6( - 4 + 3)} \right]$
$= \dfrac{1}{2}\left[ { - 15 - 6 + 6} \right]$
$= \dfrac{{ - 15}}{2}$
But the area can not be negative hence taking the positive value
area of triangle ABC${\text{ = }}\dfrac{{{\text{15}}}}{{\text{2}}}$
Therefore,
area of parallelogram ABCD=2(area of triangle ABC)
$= 2(\dfrac{{15}}{2})$
$= 15$ sq. units

Additional information: Opposite sides of a parallelogram are equal and parallel to each other, and corresponding angles are supplementary to each other.

Note: We can also find the area of the parallelogram using the formula.
Area of parallelogram ABCD=(base)(height)
Base(BA)$= \sqrt {{{(3 + 1)}^2} + {{( - 4 + 3)}^2}}$
$= \sqrt {16 + 1}$
$= \sqrt {17}$
Using a two-point form of the equation of line BA would be
i.e.$(y + 4) = \left( {\dfrac{{ - 3 + 4}}{{ - 1 - 3}}} \right)(x - 3)$
$\Rightarrow y + 4 = \dfrac{1}{{ - 4}}(x - 3)$
$\Rightarrow - 4y - 16 = x - 3$
$\Rightarrow x + 4y + 13 = 0$
The height of the parallelogram would be the perpendicular distance of D(-2,1) from BA i.e.
height $= \dfrac{{| - 2 + 4(1) + 13|}}{{\sqrt {{1^2} + {4^2}} }}$
$= \dfrac{{15}}{{\sqrt {17} }}$
Therefore, the area of parallelogram ABCD=(base)(height)
$= (\sqrt {17} )(\dfrac{{15}}{{\sqrt {17} }})$
$= 15$
Therefore, area of parallelogram= $15$ sq. units