Question

The three resistors configuration ${R_1},{R_2}$ and ${R_3}$ are connected to $3V$ battery as shown in figure. The power dissipated by the configuration ${R_1},{R_2}$ and ${R_3}$ is ${P_1},{P_2}$ and ${P_3}$ respectively. Then –

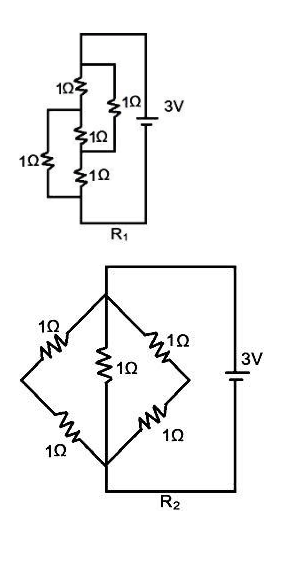
A) ${P_1} > {P_2} > {P_3}$
B) ${P_1} > {P_3} > {P_2}$
C) ${P_2} > {P_1} > {P_3}$
D) ${P_3} > {P_2} > {P_1}$

Answer 1

Hint: - Find the equivalent resistances for all the configurations in ${R_1},{R_2}$ and ${R_3}$. Now, by using the relation between power and resistance we will find the order of power in different configurations.

Complete Step by Step Solution: -
In the first configuration of ${R_1}$,

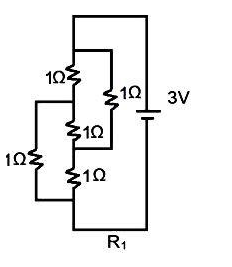
From this configuration, we can conclude that there is an equivalent wheatstone bridge circuit.
$\therefore \dfrac{{1\Omega }}{{1\Omega }} = \dfrac{{1\Omega }}{{1\Omega }} = 1\Omega$
Therefore, the equivalent resistance in the configuration ${R_1}$ is $1\Omega$.
Now, we have to calculate the equivalent resistance in the configuration ${R_2}$ -

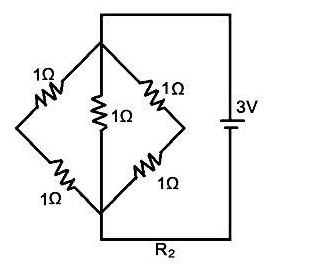
From the above figure, the equivalent resistance can be calculated by –

$$\Rightarrow {R_2} = {\left( {\dfrac{1}{{1 + 1}} + 1 + \dfrac{1}{{1 + 1}}} \right)^{ - 1}} \\\ \therefore {R_2} = {2^{ - 1}} = 0.5\Omega \\\$$

Therefore, the equivalent resistance in the configuration ${R_2}$ is $0.5\Omega$.
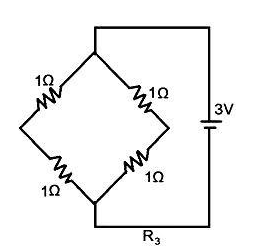
Now, we have to calculate the equivalent resistance in the configuration ${R_3}$ -

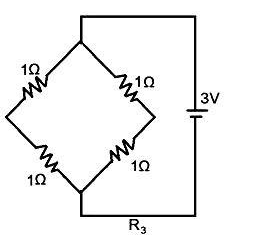
From the above figure, the equivalent resistance for the configuration ${R_3}$ is –
$\Rightarrow {R_3} = 1 + \dfrac{{\left( {1 + 1} \right)\left( {1 + 1} \right)}}{{\left( {1 + 1} \right) + \left( {1 + 1} \right)}} \\\ \therefore {R_3} = 1 + 1 = 2\Omega \\\$
Therefore, the equivalent resistance in the configuration ${R_3}$ is $2\Omega$.
We know that, relationship between power, voltage and resistance is –
$\Rightarrow P = \dfrac{{{V^2}}}{R}$
So, the power ${P_1}$ for configuration ${R_1}$ is –
$\Rightarrow {P_1} = \dfrac{{{3^2}}}{1} = 9W$
Power ${P_2}$ for configuration ${R_2}$ is –
${P_2} = \dfrac{{{3^2}}}{{0.5}} = \dfrac{9}{{0.5}} \\\ \therefore {P_2} = 18W \\\$
Power ${P_3}$ for configuration ${R_3}$ is –

$${P_3} = \dfrac{{{3^2}}}{2} = \dfrac{9}{2} \\\ \therefore {P_3} = 4.5W \\\$$

Now, we have calculated the power for each configuration for ${R_1},{R_2}$ and ${R_3}$ which are –
$\Rightarrow {P_1} = 9W \\\ \Rightarrow {P_2} = 18W \\\ \Rightarrow {P_3} = 4.5W \\\$
Therefore, we can conclude that –
${P_2} > {P_1} > {P_3}$

Hence, the correct option is (C).

Note: - Wheatstone bridge is the circuit which is connected in form of the bridge and is composed of two known resistors, one unknown resistor and one variable resistor connected in the form of a bridge. This bridge gives accurate measurements, so it is most reliable. This bridge is used for the precise measurement of low resistance and is also used to measure inductance, capacitance and impedance by using the variations.