Question
Question: The three points \(A\left( 3,8 \right)\), \(B\left( 6,2 \right)\) and \(C\left( 10,2 \right)\) are s...
The three points A(3,8), B(6,2) and C(10,2) are shown in the diagram. The point D is such that the line DA is perpendicular to AB and DC is parallel to AB. Calculate the coordinates of D.
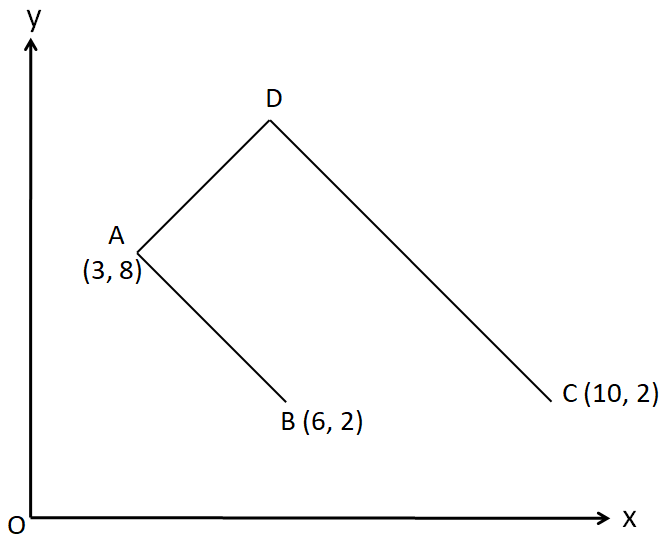
Solution
Since the coordinates of the points A and B are given, we can determine the slope of the line AB, using the formula m=x2−x1y2−y1. Since the line DC is given parallel to AB, its slope will be equal to that of AB. And since AD is given to be perpendicular to AB, the product of the slope of AB and AD will be equal to −1, from which the slope of AD can be determined. Finally, using the point-slope form, we can determine the equations for the lines AD and DC, and on solving them for x and y, we will get the required coordinates for the point D.
Complete step-by-step answer:
We know that the slope of a line passing through two points having coordinates (x1,y1) and (x2,y2) is given by
⇒m=x2−x1y2−y1
Now, the coordinates of the points A and B are respectively (3,8) and (6,2). Therefore, the slope of the line AB is given as
