Question

The three points (-2,2), (8,-2) and (-4,-3) are the vertices of
A. An isosceles triangle
B. An equilateral triangle
C. A right angled triangle
D. None of these

Answer 1

Hint: To solve this question, we should have an idea about the triangles, that for an isosceles triangle two sides are equal, for an equilateral triangle all the sides are equal and for a right angled triangle the sum of squares of two sides (base and height) must be equal to the square of the third side (hypotenuse). We will find the distance between the given points using the formula, $d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$, where $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ are the two points.

Complete step-by-step answer:
It is given in the question that, we have to identify that the three points (-2,2), (8,-2) and (-4,-3) are the vertices of which triangle. To solve this question, let us first see the conditions of triangles. We know that for an isosceles triangle the two sides must be equal, for an equilateral triangle all the sides must be equal and for a right angled triangle the sum of squares of two sides (base and height) must be equal to the square of the third side (hypotenuse). We will use the distance formula to find the distance between the given points, that is, $d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$, where $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ are the two points.
In this question we have been given three points (-2,2), (8,-2) and (-4,-3). Let us consider (-2,2) as point P, (8,-2) as point Q and (-4,-3) as point R. Now, let us consider a set of 2 points at a time in order to find the distance between them.
We can consider the points, P(-2,2) and Q(8,-2). So, the distance between these two points is given by,
$\begin{aligned} & PQ=\sqrt{{{\left( 8-\left( -2 \right) \right)}^{2}}+{{\left( -2-2 \right)}^{2}}} \\\ & PQ=\sqrt{{{\left( 10 \right)}^{2}}+{{\left( -4 \right)}^{2}}}=\sqrt{100+16} \\\ & PQ=\sqrt{116} \\\ \end{aligned}$
Now, let us consider the points, Q(8,-2) and R(-4,-3). So, the distance between these two points is given by,
$\begin{aligned} & QR=\sqrt{{{\left( -4-8 \right)}^{2}}+{{\left( -3-\left( -2 \right) \right)}^{2}}} \\\ & QR=\sqrt{{{\left( 12 \right)}^{2}}+{{\left( -1 \right)}^{2}}}=\sqrt{144+1} \\\ & QR=\sqrt{145} \\\ \end{aligned}$
Now, let us consider the points P(-2,2) and R(-4,-3). So, the distance between these two points is given by,
$\begin{aligned} & PR=\sqrt{{{\left( -4-\left( -2 \right) \right)}^{2}}+{{\left( -3-2 \right)}^{2}}} \\\ & PR=\sqrt{{{\left( -2 \right)}^{2}}+{{\left( -5 \right)}^{2}}}=\sqrt{4+25} \\\ & PR=\sqrt{29} \\\ \end{aligned}$
Now, we will check whether the triangle is isosceles, equilateral, right angled or none of these.
On comparing the distances, we get, $\sqrt{116}\ne \sqrt{145}\ne \sqrt{29}$.
From the above relation, we can say that all the sides of the triangle are of different lengths, hence it cannot be an equilateral triangle. Also, we can see that no two sides are equal, therefore it is also not an isosceles triangle. Now, we have to check whether this triangle is a right angled triangle or not. We know that for a triangle to be a right angled triangle, the sum of squares of two sides (base and height) must be equal to the square of the third side (hypotenuse).
So, we can write it as, $P{{Q}^{2}}+P{{R}^{2}}=Q{{R}^{2}}$. So, we get,
$\begin{aligned} & {{\sqrt{116}}^{2}}+{{\sqrt{29}}^{2}}={{\sqrt{145}}^{2}} \\\ & 116+29=145 \\\ & 145=145 \\\ \end{aligned}$
We can show the triangle as below.

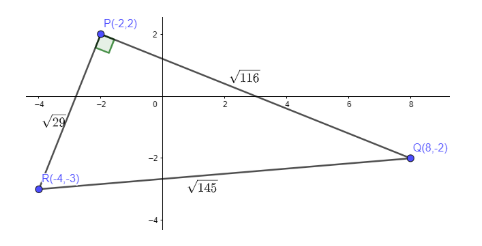
Therefore, we have satisfied the condition for a right angled triangle. Hence, we can say that the three points (-2,2), (8,-2) and (-4,-3) are the vertices of a right angled triangle. Hence, option (C) is the correct answer.

Note: The possible mistakes that the students can do in this question is the calculation mistakes. Also, the students must know the correct formula to find the distance between two points, which is, $d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$. After finding all the sides of a triangle, we get that all the sides are different, so some students tend to stop solving the question at that point and assume it as a right angled triangle and write option (c) as the correct answer. But we have to check whether the triangle is a right angled triangle or not by using the Pythagoras theorem and only then finalize the answer, as it could have also been a scalene triangle and if so option (d) would have been the correct answer.