Question
Question: The three blocks shown in figure moves with constant velocities. Find the velocity of blocks A and B...
The three blocks shown in figure moves with constant velocities. Find the velocity of blocks A and B. Given VP2=10m s−1 , VC=2m s−1 .
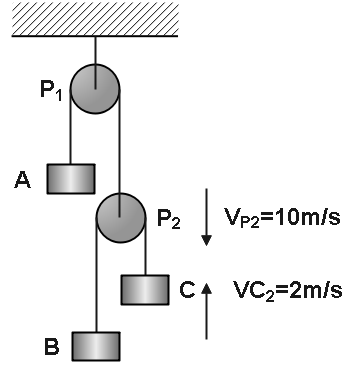
Solution
To solve this question, one must have a concept of the block pull system and Newton's law and then one can easily solve this question. But here in this question we will simply apply the trick and solve as we will assume that whenever there is decrease in length, we will take that in negative sign and whenever there is increase in length, we will take that in positive sign.
Complete Step By Step Answer:
According to the question it is given that,
The velocity of the second pulley in downward direction is, 10m s−1 and
The velocity of the block C in upward direction is, 2m s−1 .
Now, from the figure we can easily say that as the block C is going upward the block B will come downward and let us assume the velocity of the block as VB .
Simply remember the points:
Whenever there is decrease in length, we will take that in negative sign and
Whenever there is an increase in length, we will take that in a positive sign.
Now, in second pulley system,
As the block C is going up and we can see that there is a decrease in the length so we will take the velocity in negative.
Similarly, the block B is coming down and there is an increase in length so we will take the velocity in positive.
And the pulley is coming down and the length decreases so we will take it in negative . Also both points of the pulley attached with the string come down so we will take that in negative.
Now solving,
\-2−10−10+VB=0 ⇒VB=22m s−1
Now for the velocity of block A
As it is simply given that the pulley is coming downward direction with a velocity 2m s−1 so the same on the other side the block will come upward with a velocity of 10m s−1 .
Hence, the velocity of block A is 10m s−1 upward and the velocity of block B is 22m s−1 downward.
Note:
It should be emphasised that both the pulley and the rope are considered massless. As a result, the tension has been assumed to be constant throughout the string. It's also worth noting that we could use any convention of the masses travelling in a certain direction and get the same result.
