Question

The third harmonic in an open organ pipe is known as
A. Fundamental frequency
B. Second overtone
C. Third overtone
D. First overtone

Answer 1

The lowest natural frequency of a system is called Fundamental frequency, while the higher frequencies are known as Overtones. The term overtone is used to describe any resonant frequency above the fundamental frequency.

Complete step-by-step solution:
The instruments which are used to produce sound by blowing into a pipe are known as organ pipes, they are of two types; closed organ pipes, which are closed at one and open organ pipes, which are open at both ends.
For closed organ pipe,
${{f}_{0}}=\dfrac{v}{4L}$
Here, ${{f}_{0}}$ is the fundamental frequency
$v$ is the velocity of sound
$L$ is the length of the tube and $4L$ is the wavelength of the wave
${{f}_{1}}=3{{f}_{0}}$, ${{f}_{2}}=5{{f}_{0}}$ and so on
For an open organ pie,
${{f}_{0}}=\dfrac{v}{2L}$
Here, $2L$ is the wavelength of the wave
${{f}_{1}}=2{{f}_{0}}$, ${{f}_{2}}=3{{f}_{0}}$ and so on
The note produced by an open organ pipe consists of both even and odd harmonics but the notes produced by open organ pipe comprises odd harmonics only.
The lowest frequency of a periodic waveform is known as the fundamental frequency of a pipe. The higher frequencies are known as overtones.
The representation of harmonics in an open organ pipe is as follows
The A represents the antinode, and N represents the node

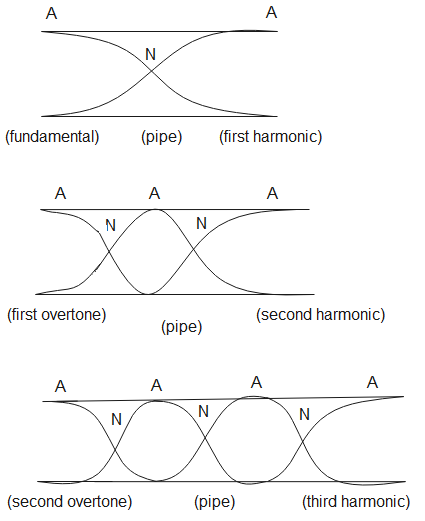
Overtone is a term used to specify any higher standing wave and the term harmonic is used for those cases in which the overtones are integral multiples of fundamental frequency.
The third harmonic in an open organ pipe is known as the second overtone. Hence, the correct option is (B).

Note: All harmonics are overtones but all overtones are not harmonics. The node is the point on the wave where resultant amplitude is zero while antinodes are those points where resultant amplitude is maximum. As the number of harmonics increase, the wavelength decreases.