Question

The thermo emf of thermocouple varies with temperature $\theta$ of the hot junction as $E=a\theta +b{{\theta }^{2}}$in volts where the ratio $\dfrac{a}{b}$ is ${{700}^{\circ }}\text{C}$. If the cold junction is kept at ${{0}^{\circ }}\text{C}$, then the neutral temperature is:
A. ${{700}^{\circ }}\text{C}$
B. ${{350}^{\circ }}\text{C}$
C. ${{1400}^{\circ }}\text{C}$
D. No neutral temperature is possible for this thermocouple

Answer 1

In the above question we are asked to determine the neutral temperature(the temperature at which the emf of a thermocouple is said to be maximum). The variation of the emf with the change in the temperature of the hot junction gives an inverted parabola whose vertex is the neutral point. Hence using this information we will determine the neural temperature of the above thermocouple.

Formula used:
$\dfrac{dE}{d\theta }=a\dfrac{d\theta }{d\theta }+b\dfrac{d{{\theta }^{2}}}{d\theta }=0$

Complete step-by-step solution:

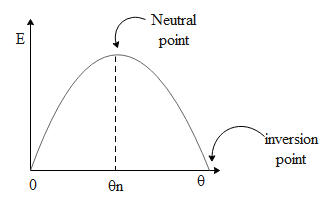
The above diagram shows the variation of the emf E across the thermocouple versus the temperature $\theta$ of the hot junction. The neutral point indicates the vertex of the inverted parabola whose coordinate on the x-axis indicates the neutral temperature. In the question it is given that the emf varies with the temperature of the hot junction via equation $E=a\theta +b{{\theta }^{2}}$. At the vertex of the above parabola, the change in the emf of the thermocouple with respect to change in the temperature is zero. Hence differentiating the equation $E=a\theta +b{{\theta }^{2}}$ with respect to $\theta$ at the neutral point we obtain the neutral temperature ${{\theta }_{n}}$ as,
$\begin{aligned} & \dfrac{dE}{d\theta }=a\dfrac{d\theta }{d\theta }+b\dfrac{d\left( {{\theta }^{2}} \right)}{d\theta } \\\ & \because \dfrac{dE}{d\theta }=0 \\\ & \Rightarrow a\dfrac{d\theta }{d\theta }+b\dfrac{d\left( {{\theta }^{2}} \right)}{d\theta }=0 \\\ & \Rightarrow a+b\left( 2{{\theta }_{n}} \right)=0 \\\ & \Rightarrow {{\theta }_{n}}=-\dfrac{a}{2b} \\\ & \because \dfrac{a}{b}={{700}^{\circ }}\text{C} \\\ & \therefore {{\theta }_{n}}=-\dfrac{{{700}^{\circ }}\text{C}}{2}=-{{350}^{\circ }}\text{C} \\\ \end{aligned}$
Since the temperature of the hot junction cannot be negative, the above thermocouple does not have a neutral temperature.
Therefore the correct answer of the above question is option D.

Note: In the above question we got the neutral temperature as negative. This does not mean that there isn’t one neutral temperature. It is just that the given data in the above question is invalid and hence we get the desired result.