Question

The thermo emf. of a hypothetical thermocouple varies with the temperature θ of hot junction as $E = a\theta + b{\theta ^2}$ in volts, where the ratio $\dfrac{a}{b}$​ is ${700^0}C$. If the cold junction is kept at ${0^0}C$, then the neutral temperature is:

A.)${700^0}C$
B.)${1400^0}C$
C.)${390^0}C$
D.)No neutral temperature is possible for this thermocouple.

Answer 1

Thermocouple is an electrical device which produces a temperature dependent voltage as a result of thermoelectric effect. The thermo emf of a thermocouple rises to a maximum at a temperature ${\theta _n}$ which is known as the neutral temperature. For a given thermocouple the neutral temperature remains constant. Since the thermo emf of a thermocouple rises to a maximum at the neutral temperature, we can use the application of derivatives to find the neutral temperature.

Formula used:
$\dfrac{{dE}}{{d\theta }} = 0$ , at $\theta = {\theta _n}$ where $E$is the thermo emf of the thermocouple and ${\theta _n}$ is the neutral temperature.

Complete step by step answer:
Thermocouple is an electrical device which produces a temperature dependent voltage as a result of thermoelectric effect. It is made of two electrical conductors (which are not similar).They are widely used as temperature sensors. It consists of two dissimilar metallic wires connected at one end and a thermocouple-capable device at the other end.

This is a general graph of thermocouple showing the variation of thermo emf with change in temperature. The cold temperature is taken as ${\theta _c}$. As we can see for small differences in temperature it is linear. But for large differences it becomes parabolic. When we increase the temperature of the hot junction, we can see that the value of thermo emf increases and reaches a maximum value at a temperature called neutral temperature denoted by ${\theta _n}$.

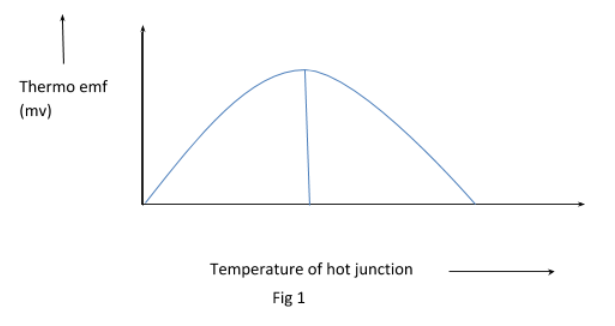
To find the neutral temperature we will find the temperature at which the derivative is zero which can be the maxima.
$E = a\theta + b{\theta ^2}$
$\dfrac{{dE}}{{d\theta }} = a + 2b\theta$
At$\theta = {\theta _n}$, $\dfrac{{dE}}{{d\theta }} = 0$
${\theta _n} = - \dfrac{a}{{2b}}$
Given in the question $\dfrac{a}{b}$=${700^0}C$,
${\theta _n} = - {350^0}C$.
Since the ${\theta _c} = {0^0}C$ negative neutral temperature is not possible. So option D is correct.

Note:
After reaching neutral temperature the thermo emf gradually decreases and reaches zero at a particular temperature known as inversion temperature. The inversion temperature is denoted by the symbol ${\theta _i}$. Beyond that the sign of thermo emf changes and increases. Note that for a given thermocouple the temperature of inversion depends on the temperature of the cold junction whereas the neutral temperature is constant.