Question

The tension in the string of a simple pendulum is
(A) Constant
(B) Maximum in the extreme position
(C) Zero in the mean position
(D) None of these

Answer 1

The bob of the pendulum undergoes vertical circular motion. So, obtain the expression for the tension in the string for vertical circular motion and check for the required conditions.

Complete step by step answer:

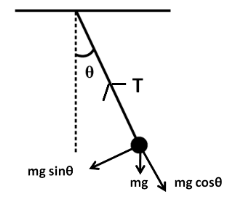
Consider a pendulum with a bob of mass $m$ , whose string is making an angle of $\theta$ with the vertical. The tension in the string, at that instant is $T$ . And the velocity of the bob at that instant is $v$ . As the bob is performing a circular motion, so from Newton's second law of motion, net force along the length of the string towards the centre should provide the required centripetal force. We have
Centripetal force, ${F_c} = \dfrac{{m{v^2}}}{R}$ (1)
where R is the length of the string.
Net force towards the centre, ${F_N} = T - mg\cos \theta$ (2)
Equating (1) and (2), we have
$\Rightarrow T - mg\cos \theta = \dfrac{{m{v^2}}}{R}$
Or, $T = \dfrac{{m{v^2}}}{R} + mg\cos \theta$ (3)
This is the expression for the tension at any instant.
As the bob performs the circular motion, the value of $\theta$ keeps changing. So, $\theta$ is not constant. Also, we know that the velocity $v$ varies from $0$ to its maximum value in the circular motion. So, $v$ is also not a constant. Hence, these two variable quantities make $T$ a variable.
$\therefore$ $T$ is not constant.
In the extreme position, the value of $\theta$ is maximum. Also, at this position the bob has zero velocity. So from (3), we have
$\Rightarrow T = \dfrac{{m{{(0)}^2}}}{R} + mg\cos {\theta _{\max }}$
Or, $T = mg\cos {\theta _{\max }}$
We know from Trigonometry that the maximum value of $\theta$ $\cos \theta$ is the minimum.
$\therefore$ T is minimum in the extreme position.
In the mean position, the value of $\theta$ is $0$ , as is evident from the figure. Also the velocity is maximum at that point, which is a non-zero value. So from (1), we can easily see that tension, T at that point is
$\Rightarrow T = \dfrac{{m{v_{\max }}^2}}{R} + mg\cos {0^ \circ }$
Or, $T = \dfrac{{m{v_{\max }}^2}}{R} + mg$
$\therefore T$ is not zero in the mean position.
So, after checking each and every option, we conclude that none of the options A, B or C are correct.
Hence, the correct answer is option (D); none of these.

Note:
For attempting these kinds of questions, always prefer to obtain the mathematical expression of the quantity concerned, as we obtained (3) in this question. Then the application of Calculus and Trigonometry will lead you to the correct answer. Don’t try to solve the question physically, as in the questions of more difficult level, you might make errors.