Question

The tension in string shown in the figure

A. Zero
B. $50N$
C. $55\sqrt 3 N$
D. $(\sqrt 3 - 1)50N$

Answer 1

Use Newton’s law of motion Find the equation of motion of the block at equilibrium. Newton’s second law of motion states that the force is equal to the mass times the acceleration of the body. The force acting on the body here is the gravity and the frictional force and the tension.

Formula used:
The equation of motion of a body at equilibrium is given by,
${F_{net}} = 0$
Where ${F_{net}}$ is the net applied force.
The limiting frictional force acting on a body at rest is given by,
${F_f} \leqslant \mu N$ where $\mu$ is the coefficient of static friction and is $N$ the normal force of the body due to the surface.

Complete step by step answer:
We have given here a block which is resting on the slanted surface and it is kept attached to a fixed surface with a string. Now, we know that the block will be at rest if the net force acting on the block is zero, ${F_{net}} = 0$ Where ${F_{net}}$ is the net applied force. Here, the forces acting on the block are the frictional force and the gravitational force. So, we can draw the force diagram as follows:

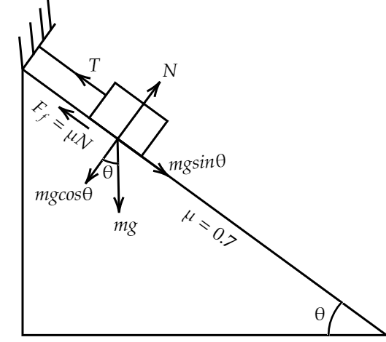
So, from the force diagram we can write,
$N = mg\cos \theta$
Putting the values $m = 10kg,\theta = {30^ \circ },g = 9.8m{s^{ - 2}}$ we will have normal force due to the surface,

\Rightarrow N= 98\dfrac{{\sqrt 3 }}{2}N$$ Now we can see that the maximum frictional force on the block is, $$\mu N = 0.7 \times 98\dfrac{{\sqrt 3 }}{2}$$............[putting $$\mu = 0.7$$, $$N = \dfrac{{98\sqrt 3 }}{2}N$$ in the equation $${F_f} = \mu N$$] $$\Rightarrow \mu N = 59.4\,N$$ And the horizontal force due to the gravity is, $$mg\sin \theta = 10 \times 9.8 \times \sin {30^ \circ }$$ $$\therefore mg\sin \theta = \dfrac{{98}}{2} = 49\,N$$ Hence, we can see that the frictional force due to the surface is greater than the horizontal force due the gravity, $$59.4N > 49N$$. Which will alone be sufficient enough to keep the block at rest. Hence, the tension in the string must be zero. So, the tension in the string is zero. **Hence, option A is the correct answer.** **Note:** Since the frictional force is greater than the horizontal force due to the gravity, the block can be given more force up to a value of $$59.4 - 49 = 10.4N$$ and will still be at rest. If a horizontal force is applied to the block and is greater than $$\mu N - mg\sin \theta $$ or $$10.4\,N$$there will be a tension in the string.