Question

The tension in a string holding a solid block of density $\rho_S$ below the surface of a liquid of density $\rho_l\;(\rho_l > \rho_S)$ is $T_0$ when the beaker is at rest. Tension in the string when the beaker moves up with acceleration $a$ is:
A. $T=0$
B. $T=T_0$
C. $T=T_0\left[1+\dfrac{a}{g}\right]$
D. $T=T_0\left[1-\dfrac{a}{g}\right]$

Answer 1

An easy way to go about understanding the forces at play is to sketch out a free body diagram for both the cases. Remember to account for the tension in the string, the weight of the block, and the buoyant force exerted by the liquid. Also remember that the weight of the liquid displaced gives the magnitude of the buoyant force.
Once you have summarized all the forces acting in both the cases and the consequences that the acceleration in the second case has on the buoyant force and weight of the block, just rearrange the free body equation in the second case such that it can be expressed in terms of free body expressions derived in the first case and this should give you a relation between tension in the string in both cases.

Formula used: Buoyant force exerted by a liquid at rest $F_{buoyant} = m_{liquid}g = V\rho_l g$, where $m_{liquid}$ and $\rho_l$ are mass and density of the liquid, V is the volume of the liquid displaced, and g is the acceleration due to gravity.

Complete step by step answer:
We have a beaker filled with liquid of density $\rho_l$, and a string holds up a block of density $\rho_s$ below the surface of the liquid. Let the volume of the block be $V$. Then, the volume of water displaced by the liquid as a consequence of this block is also $V$.
Therefore, the buoyant force $F_{buoyant}$ exerted by the liquid of the block is given as:
$F_{buoyant} = m_{liquid}g = V\rho_l g$, since mass is volume times density.
The weight of the block can be given as:
$W_{block} = m_{block}g = V\rho_s g$
Let us begin with an evaluation of the first case where the beaker is at rest.

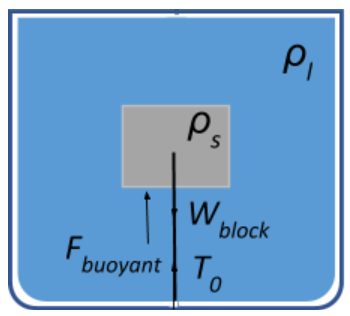
When the beaker is at rest, and the block is immersed in the liquid, the block in the beaker is at equilibrium. This means that the net force on the block is zero.
That is, $W_{block} + T_0 = F_{Buoyant}$
$\Rightarrow V\rho_s g + T_0 = V\rho_l g$
$\Rightarrow T_0 = V\rho_l g - V\rho_s g$
$\Rightarrow \dfrac{T_0}{g} = V\rho_l - V\rho_s$
Now let us look at the case when the beaker is accelerated upwards.
When the beaker is accelerated upwards, there is an increase in the buoyant force due to an increased displacement of the liquid.
Thus, $F_{buoyant} = V\rho_l (g+a)$, and hence, the net weight of the block is given as:
$W_{net\;block} = m_{block}(g+a) – m_{block}g = m_{block}a = V\rho_s a$

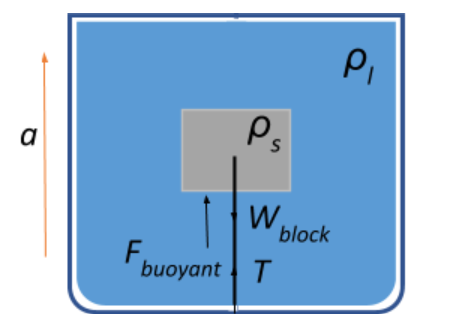
Now, balancing the forces:
$W_{net\;block} = F_{buoyant} – W_{block} - T$
$\Rightarrow V\rho_s a = V\rho_l (g+a) - V\rho_s g -T$
$\Rightarrow 0 = (V\rho_l g – V\rho_s g) + (V\rho_l – V\rho_s)a -T$
From the first case, we got that $V\rho_l g - V\rho_s g =T_0$ and $V\rho_l - V\rho_s =\dfrac{T_0}{g}$.
Substituting these in our equation, we get:
$\Rightarrow 0 = T_0 + \left(\dfrac{T_0}{g}\right)a -T$
$\Rightarrow T = T_0\left(1 +\dfrac{a}{g}\right)$

So, the correct answer is “Option C”.

Note: Always use free body diagrams to summarize the list of all influencing forces in a system as this ensures that all forces are accounted for.
Also, on a specific note, do not forget that the magnitude of buoyant force can be derived by calculating the weight of the fluid displaced. Thus, buoyancy is directly proportional to the density of the immersed fluid.