Question

The tension in a string holding a solid block below the surface of a liquid (where ${\rho _{liquid}} > {\rho _{block}}$) as shown in the figure is $T$when the system is at rest. Then what will be the tension in the string if the system has upward acceleration $a$?

(A) $T(1 - \dfrac{a}{g})$
(B) $T(1 + \dfrac{a}{g})$
(C) $T(\dfrac{a}{g} - 1)$
(D) $\dfrac{a}{g}T$

Answer 1

Firstly we have to draw a free body diagram showing all the forces in the system in both cases. First, when the system is at rest. Second when the system is moving with acceleration $a$. The forces that are involved in both the cases are the tension force in the string acting upwards, the weight of the block acting downwards and the buoyant force exerted by the liquid. The magnitude of the buoyant force can be calculated by finding the weight of the liquid displaced when the block is put in the liquid. After finding the equations for the sum of all the forces in both the cases we rearrange the second equation in a manner that we can express it in terms of equation one. This will give us the relation between tensions in both cases.

Formula used:
Buoyant force, ${F_{buoyant}} = {m_l}g = v{\rho _l}g$, where ${m_l},v,g,{\rho _l}$ are the mass of liquid, the volume displaced, gravity, the density of liquid respectively.

Complete step by step solution: From the question we know that the block is below the surface of the water and assuming the volume of the block as $v$ then the volume of water displaced will be $v$.
From the formula of buoyant force, ${F_{buoyant}} = {m_l}g = v{\rho _l}g$(because Mass = Volume \times Density)$The equation for the first case where there is no acceleration when the system is at rest. Free body diagram of the first case,  When it is at rest it means the block is at equilibrium with respect to the beaker. This tells us that the net force is zero on the block.${w_b}, T,{\rho s}$are the weight of the block, the tension in the string at rest, the density of the block (solid).$ {w_b} + T = {F{buoyant}} $$v{\rho _S}g + T = v{\rho _L}g $$\dfrac{T}{g} = v{\rho _l} - v{\rho _s} $
The equation for the second case when the system is moving with acceleration upwards, this causes an increase in buoyant force due to increased displacement of liquid.
Free body diagram in the second case,

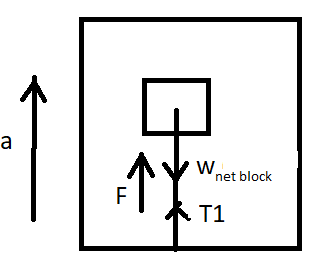
${F_{buoyant}} = v{\rho _l}(g + a)$
${w_{block}} = {m_b}(g + a) - {m_b}g$
${m_b}a = v{\rho _s}a$
By balancing the forces we get, ${T_1}$ is the tension in the string when the system is being accelerated. ${w_{netblock}}$is the weight of the block while the system is being accelerated.
${w_{netblock}} = {F_{buoyant}} - {w_b} - {T_1}$
$v{\rho _s}a = v{\rho _l}(g + a) - v{\rho _s}g - {T_{_1}}$
$0 = (V{\rho _l}g - v{\rho _s}g) + (v{\rho _l} - v{\rho _s})a - {T_1}$
Substituting the first equation, $v{\rho _l}g - v{\rho _s}g = T$ in second, We get,
$T + (\dfrac{T}{g})a = {T_1}$
${T_1} = T(1 + \dfrac{a}{g})$

Hence, the correct option is (B), $T(1 + \dfrac{a}{g}).$

Note: Always remember that the buoyant force can be derived from the weight of the liquid displaced, which is why the density of the liquid is directly proportional to the buoyant force. Because the system is being accelerated upwards the buoyant force increases, on the other hand, if the system is being accelerated downwards then the buoyant force decreases.