Question
Question: The temperature \(\left( \theta \right)\) of “cup of coffee” in a BARISTA restaurant was plotted as ...
The temperature (θ) of “cup of coffee” in a BARISTA restaurant was plotted as a function of time. Which of the following curves may represent the plot?
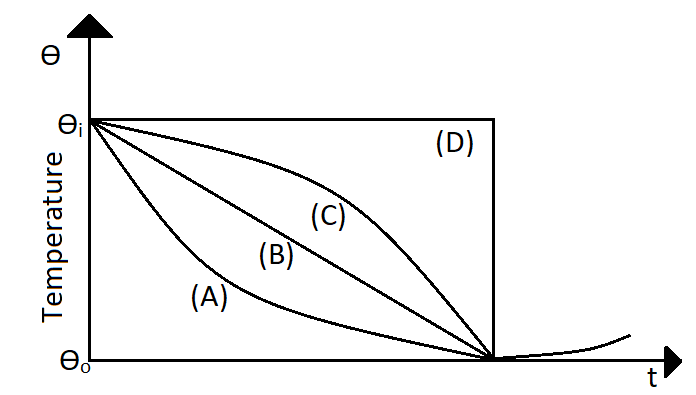
Solution
Hint
According to Newton’s law of cooling, we can state that the rate of heat loss of a body is directly proportional to the difference in temperature between the body and its surroundings and decays exponentially. So the graph will be of exponential decay.
Complete step by step answer
In the question, it is said that the temperature of a cup of coffee was plotted as a function of time. Now as time increases the temperature of the coffee decreases. This will be given by Newton’s law of cooling. According to the law, the rate of the decrease in temperature of a body is directly proportional to the difference between its temperature and the temperature of the environment. So the mathematical form of the law will be,
dtdT(t)∝(T−Tenv) where T(t) is the temperature of the coffee in time t and Tenv is the temperature of the surrounding environment.
Therefore removing the proportionality, dtdT(t)=−k[T(t)−Tenv] where k is the constant of proportionality.
Now let us consider the initial temperature of the coffee as, To. So the difference in the temperature of the coffee and the surroundings initially is,
yo=To−Tenv
And the difference between the temperatures at the time t is,
y(t)=T(t)−Tenv
By differentiating this equation on both sides with respect to t we get,
dtdy(t)=dtd[T(t)−Tenv]
Since the temperature of the environment is almost constant with time, so differentiating it gives 0.
∴dtdy(t)=dtdT(t)
From Newton’s law of cooling, we can write,
dtdy(t)=−k[T(t)−Tenv]
Now since, y(t)=T(t)−Tenv, so
dtdy(t)=−ky(t)
The solution of these type of differential equations are given as,
y(t)=yoe−kt
So substituting the values we have,
T(t)−Tenv=(To−Tenv)e−kt
Therefore we get,
T(t)=Tenv+(To−Tenv)e−kt
Therefore the temperature is an exponential function of time. So the in the graph the temperature decays exponentially with time and we get,
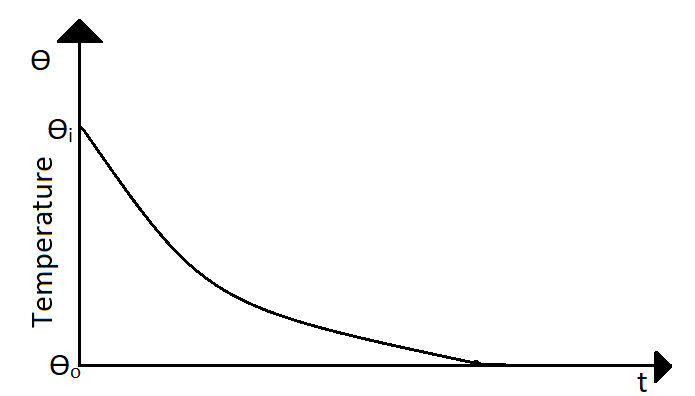
Therefore the correct answer will be option (A).
Note
Newton’s law of cooling can be applied in various cases to find the time with the help of the change in any substance’s temperature. It is specifically very applicable to crime scenes in finding time with a difference in temperature.
