Question
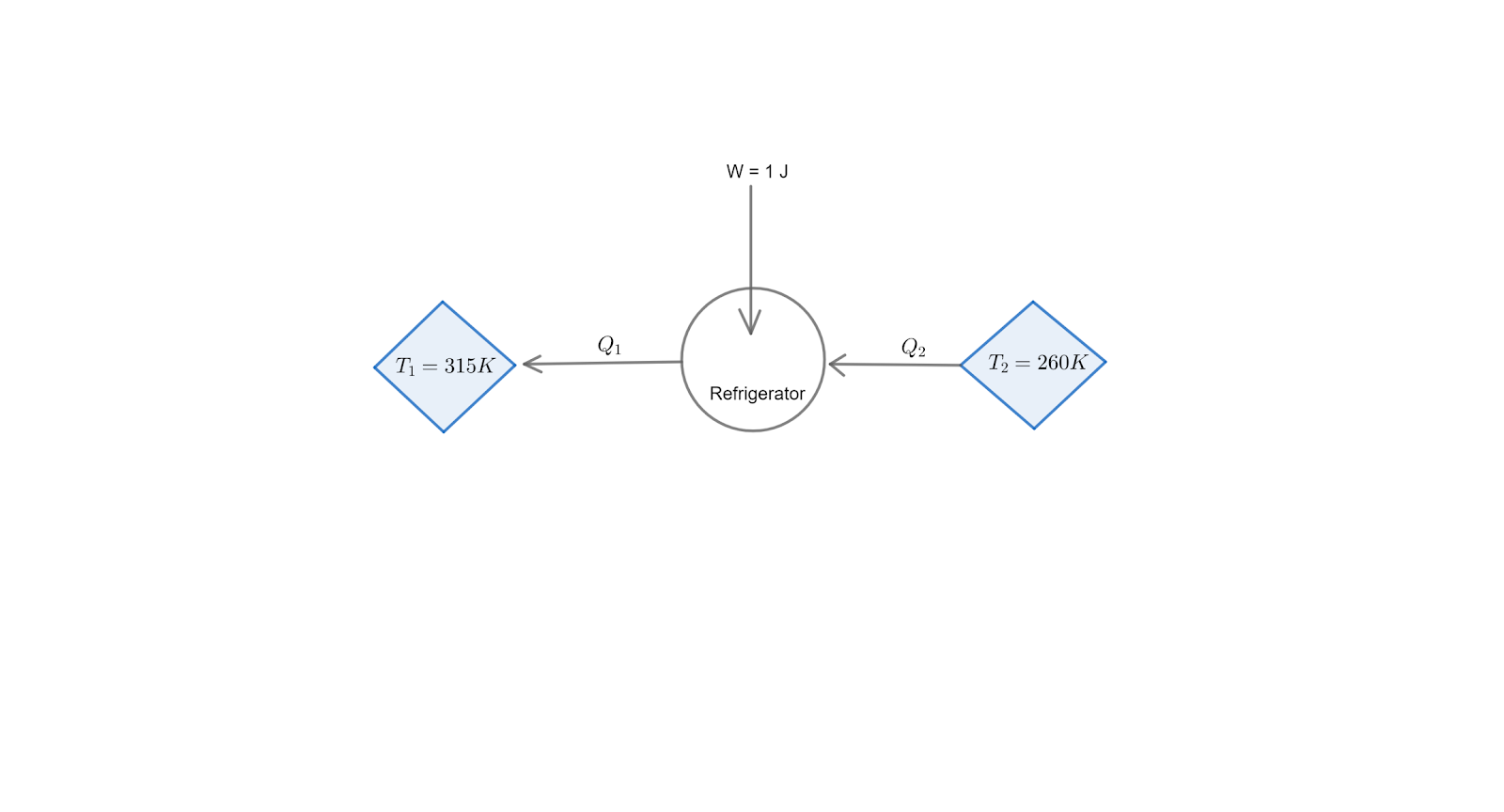
Question: The temperature inside & outside of the refrigerator is 260 K and 315 K respectively. Assuming that ...
The temperature inside & outside of the refrigerator is 260 K and 315 K respectively. Assuming that the refrigerator cycle is reversible, calculate the heat delivered to the surrounding for every joule of work done.
Solution
Hint Here, we are given the inside and outside temperature of a refrigerator. The inside of a refrigerator should be treated as a sink and the outside of the refrigerator should be taken as the source. We need to find the amount of heat delivered per unit work done. For that we first need to find the amount of heat extracted from the fridge per unit work.
Complete step by step solution
The reversible refrigeration cycle is the ideal reverse Carnot cycle or Carnot refrigeration cycle. A Carnot refrigerator is a device that removes heat (Q2) from the low temperature source or the inside of the refrigerator (T2) to a higher temperature (T1) sink or the outside of the refrigerator by using mechanical work (W).
Where Q1 is the heat delivered to the surroundings
and Q2 is the heat extracted from the refrigerator
The work done by the refrigerator, W=Q2−Q1.
Now, the coefficient of performance of a Carnot refrigerator is given by:
β=WQ2=T2−T1T2 ---- (1)
Where, T2 is the temperature of the refrigerator, i.e. inside of the refrigerator
T1 is the temperature of the surroundings, i.e. outside of the refrigerator
In the question, we are given T1 = 315 K and T2 = 260 K. Putting these values in equation (1),
⇒WQ2=T2−T1T2 ⇒WQ2=315−260260 ⇒WQ2=55260 ⇒WQ2=1152
Now, we have to find the heat delivered to the surrounding for every joule of work done. For this we will take work done, W=1J.
⇒1Q2=1152 ⇒Q2=4.72727 ⇒Q2≈4.73
This is the heat extracted from the refrigerator per joule of work done. We need to find the heat delivered to the surroundings for every 1J of work done, i.e. we need to find Q1 for W=1J.
∵W=Q2−Q1 ⇒Q1=Q2+W ⇒Q1=4.73+1 ⇒Q1=5.73
Therefore, the heat delivered to the surrounding for every joule of work done will be 5.73 J.
Note: Here is the basic diagram for the given reversible /carnot refrigerator for better understanding of the problem :