Question
Question: The temperature difference of \({120^ \bullet }C\) is maintained between two ends of a uniform rod A...
The temperature difference of 120∙C is maintained between two ends of a uniform rod AB of length 2L. Another bent rod PQ of the same cross section as AB and length 23L, is connected across AB (see figure). In steady state, the temperature difference between P and Q will be close to:
A) 60∙C
B) 75∙C
C) 35∙C
D) 45∙C
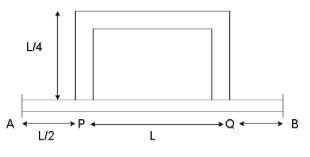
Solution
Temperature difference describes the total amount of internal energy stored in the system. It is the measure of hotness or coldness of a body. If two bodies are at the same temperature then there will be no flow of heat between them.
Complete step by step answer:
Step I:
Given that temperature difference is maintained between the rod AB, this means that there will be some resistance offered to the flow of electrons or charged particles. The resistance of wire AB is given by
R=AρL
Where ρ is the constant of resistivity
L is the length of the rod
A is the area of cross section
In this case, the constant of resistivity and area of the cross section will be the same throughout. Therefore,
R∝L
Step II:
In rod AB, part AP of the rod has length given 2L
So, resistance will be =2R
Part PQ of the rod has given lengthL
Therefore, resistance =R
Part QB will also have length similar to PA =2L
So, its resistance will be=2R
Step III:
In rod AB all the resistors are connected in series. Therefore equivalent resistance, across PQ is
(Req)PQ=4R+R+4R
(Req)PQ=46R
(Req)PQ=23R
Step IV:
The part PQ of the rod is parallel to the bent rod. Therefore resistance across the bent rod will also be R .
These resistors are parallel. Therefore their resistance will be calculated using the formula,
Req=R1+R2R1×R2
Here R1=23R,R2=R
Req=23+R23×R
Req=23R×52R
Req=53R2
Step V:
Using Ohm’s Law, V=IR
I=RV
Therefore,
Current through part of wire AB = Current through part of wire PQ
2R+2R+53RVB−VA=53RVQ−VP
R+53RVB−VA=53RVQ−VP
58RVB−VA=53RVQ−VP ---(i)
Step VI:
Since, current flows in the circuit due to potential difference. But heat flows due to temperature difference. Therefore, in equation (i) replacing potential difference with temperature difference,
58RTB−TA=53RTQ−TP
Given temperature difference, TB−TA=120
Substituting the values,
58R120=53RTQ−TP
TQ−TP=83×120
TQ−TP=45∙C
Option D is the right answer.
Note:
It is to be noted that resistance and resistivity are not the same. They are completely different terms. Resistance is the opposition to the flow of current, but resistivity is the resistance offered by the material per unit area of the material.
