Question

The tangents drawn from the point (– 8, 0) to the parabola ${y^2} = 8x$ touch the parabola at P and Q. If F is the focus of the parabola, then what is the area of the triangle PFQ (in sq. units)?
(a). 48
(b). 32
(c). 24
(d). 64

Answer 1

Hint: Find the equation of the chord PQ which is the chord of contact of tangents drawn from the point A. Then find the base and height of the triangle PFQ and find the area of the triangle PFQ.

Complete step by step solution:

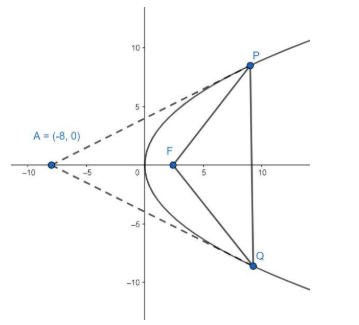
We can see in the figure that the two tangents drawn from the point A (-8, 0) intersects the parabola at P and Q.
We know that the equation of chord of contact of the tangents drawn from the point (a, b) to the parabola ${y^2} = 4ax$ is given as follows:
$yb = 4a(x + a)..........(1)$
From equation (1), the equation of chord of contact of the tangents drawn from the point A (-8, 0) is given as follows:
$0 = 8(x - 8)$
$x = 8$
Hence, the equation of line PQ is x = 8.
The line PQ intersects the parabola at points P and Q.
${y^2} = 8(8)$
$y = \pm 8$
Hence, the point P is (8, 8) and the point Q is (-8, 8).
The focus of the parabola ${y^2} = 4ax$ is (a, 0).
Hence, the point F is (2, 0).
The base of the triangle PFQ is PQ.
PQ = $8 - ( - 8)$
PQ = 16 units
The height of the triangle PFQ is given by:
Height = $8 - 2$
Height = 6 units.
Hence, the area of the triangle is given by:
Area = $\dfrac{1}{2}bh$
Area = $\dfrac{1}{2}(16)(6)$
Area = 48 sq. units
Hence, the correct answer is option (a).

Note: If you choose the base as 8 units by mistake, then the area of the triangle will turn out to be half of the answer of 48, that is, 24 sq. units and you will choose option (c), which is wrong.