Question

The tangents drawn from a point P to the ellipse make an angle ${{\theta }_{1}}$ and ${{\theta }_{2}}$ with the major axis; find the locus of P when,
$\tan {{\theta }_{1}}-\tan {{\theta }_{2}}$ is constant $=d$

Answer 1

First write down the general equation of the ellipse and then the standard equation of tangent for ellipse for the tangent $y=mx\pm \sqrt{{{a}^{2}}{{m}^{2}}+{{b}^{2}}}$ , Let there be a point $P\left( h,k \right)$ that lies on that tangent. Now rewrite the tangent equation for the point $P\left( h,k \right)$ and then evaluate to form a quadratic expression in ‘m’ and proceed further to find the sum of roots, $\tan {{\theta }_{1}}+\tan {{\theta }_{2}}$ and then from there find the value of $\tan {{\theta }_{1}}-\tan {{\theta }_{2}}$

Complete step by step solution:
Let us write the general equation for an ellipse.
It is given by,
$\Rightarrow \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ considered that $\left( a>b \right)$
Hence, X-axis is the major axis.

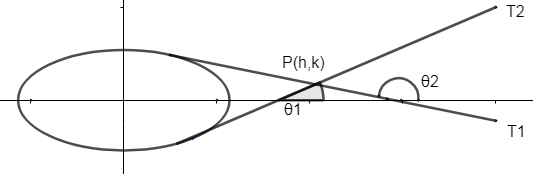
As we have the equation of tangent drawn from an external point with given slope is
$y=mx\pm \sqrt{{{a}^{2}}{{m}^{2}}+{{b}^{2}}}$
The slope of the tangent ${{T}_{1}}=\tan {{\theta }_{1}}$
And the slope of the tangent ${{T}_{2}}=\tan {{\theta }_{2}}$
Let us consider a point $P\left( h,k \right)$ that lies on this tangent.
We can rewrite the tangent equation as,
$\Rightarrow k=mh\pm \sqrt{{{a}^{2}}{{m}^{2}}+{{b}^{2}}}$
$\Rightarrow {{\left( k-mh \right)}^{2}}={{a}^{2}}{{m}^{2}}+{{b}^{2}}$
$\Rightarrow {{k}^{2}}+{{m}^{2}}{{h}^{2}}-2mkh={{a}^{2}}{{m}^{2}}+{{b}^{2}}$
$\Rightarrow {{m}^{2}}\left( {{h}^{2}}-{{a}^{2}} \right)-2mhk+{{k}^{2}}-{{b}^{2}}=0$
As m is a quadratic function, hence it has two roots or two tangents passing through P are there with slopes $\tan {{\theta }_{1}}$ and $\tan {{\theta }_{2}}$
Hence, $\tan {{\theta }_{1}}$ and $\tan {{\theta }_{2}}$ are roots of quadratic obtained.
The sum of roots for the quadratic equation is given by,
The Sum of roots is given by $=\dfrac{-b}{a}$ in $a{{x}^{2}}+bx+c=0$
$\Rightarrow \tan {{\theta }_{1}}+\tan {{\theta }_{2}}=\dfrac{2hk}{{{h}^{2}}-{{a}^{2}}}$
And the product of roots is given by,
Product of roots is given by $\dfrac{c}{a}$ in $a{{x}^{2}}+bx+c=0$
$\Rightarrow \tan {{\theta }_{1}}\tan {{\theta }_{2}}=\dfrac{{{k}^{2}}-{{b}^{2}}}{{{h}^{2}}-{{a}^{2}}}$
We also know that,
$\Rightarrow {{\left( a+b \right)}^{2}}={{\left( a-b \right)}^{2}}+4ab$
Substituting the slopes, we get,
$\Rightarrow {{\left( \tan {{\theta }_{1}}-\tan {{\theta }_{2}} \right)}^{2}}={{\left( \tan {{\theta }_{1}}+\tan {{\theta }_{2}} \right)}^{2}}+4\tan {{\theta }_{1}}\tan {{\theta }_{2}}$
As $\tan {{\theta }_{1}}-\tan {{\theta }_{2}}=d$ (given)
$\Rightarrow {{d}^{2}}={{\left( \dfrac{2hk}{{{h}^{2}}-{{a}^{2}}} \right)}^{2}}+4\left( \dfrac{{{k}^{2}}-{{b}^{2}}}{{{h}^{2}}-{{a}^{2}}} \right)$
On further evaluating we get,
$\Rightarrow {{d}^{2}}=\dfrac{4{{h}^{2}}{{k}^{2}}}{{{\left( {{h}^{2}}-{{a}^{2}} \right)}^{2}}}+4\left( \dfrac{{{k}^{2}}-{{b}^{2}}}{{{h}^{2}}-{{a}^{2}}} \right)$
$\Rightarrow {{d}^{2}}=\dfrac{4{{h}^{2}}{{k}^{2}}-4\left( {{h}^{2}}-{{a}^{2}} \right)\left( {{k}^{2}}-{{b}^{2}} \right)}{{{\left( {{h}^{2}}-{{a}^{2}} \right)}^{2}}}$
$\Rightarrow {{d}^{2}}{{\left( {{h}^{2}}-{{a}^{2}} \right)}^{2}}=4{{h}^{2}}{{k}^{2}}+4\left( {{k}^{2}}-{{b}^{2}} \right)\left( {{h}^{2}}-{{a}^{2}} \right)$
$\Rightarrow {{d}^{2}}{{\left( {{h}^{2}}-{{a}^{2}} \right)}^{2}}=4\left( {{h}^{2}}{{k}^{2}}-{{h}^{2}}{{k}^{2}}+{{a}^{2}}{{k}^{2}}+{{h}^{2}}{{b}^{2}}-{{a}^{2}}{{b}^{2}} \right)$
On simplifying,
$\Rightarrow {{d}^{2}}{{\left( {{h}^{2}}-{{a}^{2}} \right)}^{2}}=4\left( {{a}^{2}}{{k}^{2}}+{{h}^{2}}{{b}^{2}}-{{a}^{2}}{{b}^{2}} \right)$
Replacing (h, k) by (x, y) to get locus: -
$\Rightarrow {{d}^{2}}{{\left( {{x}^{2}}-{{a}^{2}} \right)}^{2}}=4\left( {{x}^{2}}-{{a}^{2}} \right)\left( {{y}^{2}}-{{b}^{2}} \right)+4{{x}^{2}}{{y}^{2}}$
Now the required locus is ${{d}^{2}}{{\left( {{x}^{2}}-{{a}^{2}} \right)}^{2}}=4\left( {{x}^{2}}-{{a}^{2}} \right)\left( {{y}^{2}}-{{b}^{2}} \right)+4{{x}^{2}}{{y}^{2}}$

Note: Eliminating ${{\theta }_{1}}\And {{\theta }_{2}}$ by using the given relation ${{\tan }^{2}}{{\theta }_{1}}+{{\tan }^{2}}{{\theta }_{1}}=\lambda$ with the help of quadratic formed in ‘m’ i.e. $y=mx\pm \sqrt{{{a}^{2}}{{m}^{2}}+{{b}^{2}}}$ or ${{\left( y-mx \right)}^{2}}={{a}^{2}}{{m}^{2}}+{{b}^{2}}$ by using properties of roots is the key point of this equation.