Question
Question: The tangent to the curve $y=x^2e^x$ at $(2,4e^2)$ also passes through the point....
The tangent to the curve y=x2ex at (2,4e2) also passes through the point.
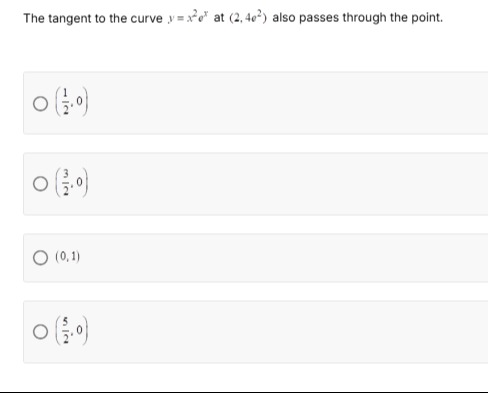
(21,0)
(23,0)
(0,1)
(25,0)
(23,0)
Solution
To find the point through which the tangent to the curve y=x2ex at (2,4e2) also passes, we follow these steps:
-
Find the derivative of the curve:
Given the curve y=x2ex.
Using the product rule, dxdy=dxd(x2)ex+x2dxd(ex).
dxdy=2xex+x2ex
Factor out ex:
dxdy=ex(2x+x2) -
Calculate the slope of the tangent at the given point (2,4e2):
Substitute x=2 into the derivative:
m=(dxdy)x=2=e2(2(2)+22)
m=e2(4+4)
m=8e2 -
Determine the equation of the tangent line:
The equation of a line passing through a point (x1,y1) with slope m is given by y−y1=m(x−x1).
Here, (x1,y1)=(2,4e2) and m=8e2.
So, the equation of the tangent line is:
y−4e2=8e2(x−2)
y−4e2=8e2x−16e2
y=8e2x−16e2+4e2
y=8e2x−12e2 -
Check which of the given options satisfies the tangent line equation:
-
Option 1: (21,0)
Substitute x=21, y=0:
0=8e2(21)−12e2
0=4e2−12e2
0=−8e2 (False) -
Option 2: (23,0)
Substitute x=23, y=0:
0=8e2(23)−12e2
0=12e2−12e2
0=0 (True)
-
Since this option satisfies the equation, it is the correct answer.
