Question

The tangent to the circle ${{x}^{2}}+{{y}^{2}}=5$ also touches the circle
[a] ${{x}^{2}}+{{y}^{2}}-8x+6y-20=0$
[b] ${{x}^{2}}+{{y}^{2}}-8x+6y+20=0$
[c] ${{x}^{2}}+{{y}^{2}}+8x+6y-20=0$
[d] ${{x}^{2}}+{{y}^{2}}-8x+9y-20=0$

Answer 1

Use the fact that the equation of the tangent to any second degree conic $a{{x}^{2}}+2hxy+b{{y}^{2}}+2gx+2fy+c=0$ at point $\left( {{x}_{1}},{{y}_{1}} \right)$ on the conic can be obtained by replacing ${{x}^{2}}$ by $x{{x}_{1}}$, ${{y}^{2}}$ by $y{{y}_{1}},xy$ by $\dfrac{x{{y}_{1}}+{{x}_{1}}y}{2},x$ by $\dfrac{x+{{x}_{1}}}{2}$ and $y$ by $\dfrac{y+{{y}_{1}}}{2}$. Hence find the equation of the tangent to the circle ${{x}^{2}}+{{y}^{2}}=5$ at point (1,-2). Use the fact that the line $ax+by+c=0$ is tangent to the circle with centre $\left( h,k \right)$ and radius r if and only if the distance of the line from the centre is equal to the radius, i.e. $\dfrac{\left| ah+bk+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}=r$. Hence determine which of the circles in the options can have the line as its tangent.

Complete step-by-step answer:

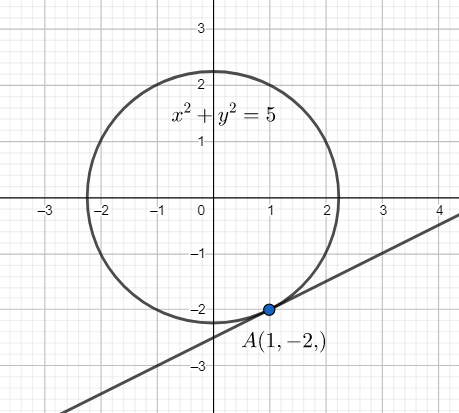
We have the equation of the circle is ${{x}^{2}}+{{y}^{2}}=5$
We know that the equation of the tangent to any second degree conic $a{{x}^{2}}+2hxy+b{{y}^{2}}+2gx+2fy+c=0$ at point $\left( {{x}_{1}},{{y}_{1}} \right)$ on the conic can be obtained by replacing ${{x}^{2}}$ by $x{{x}_{1}}$, ${{y}^{2}}$ by $y{{y}_{1}},xy$ by $\dfrac{x{{y}_{1}}+{{x}_{1}}y}{2},x$ by $\dfrac{x+{{x}_{1}}}{2}$ and $y$ by $\dfrac{y+{{y}_{1}}}{2}$.
Here ${{x}_{1}}=1$ and ${{y}_{1}}=-2$
Hence the equation of the tangent is
$\begin{aligned} & x\left( 1 \right)+y\left( -2 \right)=5 \\\ & \Rightarrow x-2y=5 \\\ \end{aligned}$
Subtracting 5 from both sides, we get
$x-2y-5=0$
We know that the line $ax+by+c=0$ is tangent to the circle with centre $\left( h,k \right)$ and radius r if and only if the distance of the line from the centre is equal to the radius. Hence determine which of the circle in the options can have the line as its tangent, i.e. $\dfrac{\left| ah+bk+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}=r$
Checking option [a]:
Equation of the circle is ${{x}^{2}}+{{y}^{2}}-8x+6y-20=0$
We know that the centre of the circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ is $\left( -g,-f \right)$ and the radius is $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$
Hence the centre of the circle is (4,-3) and the radius is $\sqrt{{{4}^{2}}+{{3}^{2}}+20}=\sqrt{45}=3\sqrt{5}$
Also, the distance of the line $x-2y-5=0$ from (4,-3) is $\dfrac{\left| 4-3\left( -2 \right)-5 \right|}{\sqrt{{{2}^{2}}+{{1}^{2}}}}=\dfrac{5}{\sqrt{5}}=\sqrt{5}$ which is not equal to the radius of the circle.
Hence the line $x-2y-5=0$ is not tangent to the circle ${{x}^{2}}+{{y}^{2}}-8x+6y-20=0$
Checking Option [b]
Equation of the circle is ${{x}^{2}}+{{y}^{2}}-8x+6y+20=0$
We know that the centre of the circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ is $\left( -g,-f \right)$ and the radius is $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$
Hence the centre of the circle is (4,-3) and the radius is $\sqrt{{{4}^{2}}+{{3}^{2}}-20}=\sqrt{5}$
Also, the distance of the line $x-2y-5=0$ from (4,-3) is $\dfrac{\left| 4-3\left( -2 \right)-5 \right|}{\sqrt{{{2}^{2}}+{{1}^{2}}}}=\dfrac{5}{\sqrt{5}}=\sqrt{5}$ which is t equal to the radius of the circle.
Hence the line $x-2y-5=0$ is tangent to the circle ${{x}^{2}}+{{y}^{2}}-8x+6y+20=0$
Checking Option [c]
Equation of the circle is ${{x}^{2}}+{{y}^{2}}+8x+6y-20=0$
We know that the centre of the circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ is $\left( -g,-f \right)$ and the radius is $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$
Hence the centre of the circle is (-4,-3) and the radius is $\sqrt{{{4}^{2}}+{{3}^{2}}+20}=\sqrt{45}=3\sqrt{5}$
Also, the distance of the line $x-2y-5=0$ from (4,-3) is $\dfrac{\left| -4-3\left( -2 \right)-5 \right|}{\sqrt{{{2}^{2}}+{{1}^{2}}}}=\dfrac{3}{\sqrt{5}}$ which is not equal to the radius of the circle.
Hence the line $x-2y-5=0$ is not tangent to the circle ${{x}^{2}}+{{y}^{2}}+8x+6y-20=0$
Checking Option [d]
Equation of the circle is ${{x}^{2}}+{{y}^{2}}-8x+9y-20=0$
We know that the centre of the circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ is $\left( -g,-f \right)$ and the radius is $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$
Hence the centre of the circle is $\left( 4,\dfrac{-9}{2} \right)$ and the radius is $\sqrt{{{4}^{2}}+{{\left( \dfrac{9}{2} \right)}^{2}}+20}=\dfrac{1}{2}\sqrt{225}=\dfrac{15}{2}$
Also, the distance of the line $x-2y-5=0$ from $\left( 4,\dfrac{-9}{2} \right)$ is $\dfrac{\left| 4-\dfrac{9}{2}\left( -2 \right)-5 \right|}{\sqrt{{{2}^{2}}+{{1}^{2}}}}=\dfrac{1}{2}\dfrac{21}{\sqrt{5}}=\dfrac{21}{2\sqrt{5}}$ which is not equal to the radius of the circle.
Hence the line $x-2y-5=0$ is not tangent to the circle ${{x}^{2}}+{{y}^{2}}-8x+9y-20=0$

So, the correct answer is “Option b”.

Note: [1] We can find the equation of the tangent of the circle using the fact that the line joining the centre of the circle and the point of the contact is normal to the circle.
We know that the centre of the circle ${{x}^{2}}+{{y}^{2}}=5$ is (0,0)
Slope of the line joining (0,0) and (1,-2) is $\dfrac{-2-0}{1-0}=-2$
We know that the product of slope of two perpendicular lines is -1.
Hence, the slope of the tangent is $\dfrac{1}{2}$
Hence the equation of the tangent is
$y+2=\dfrac{1}{2}\left( x-1 \right)$
Multiplying both sides by 2, we get
$x-1=2y+4$
Subtracting $2y+4$ from both sides, we get
$x-2y-5=0$ which is the same as obtained above.