Question

The tangent PT and the normal PN to the parabola ${{y}^{2}}=4ax$ at a point P on it meet its axis at points T and N, respectively. The locus of the centroid of the $\Delta PTN$ is a parabola. Find the characteristics of the parabola.
A. vertex = $\left( \dfrac{2a}{3},0 \right)$
B. directrix is $x=0$
C. latus rectum = $\dfrac{2a}{3}$
D. focus = $\left( a,0 \right)$

Answer 1

From the given equation of parabola we find out the equation of normal and tangent at the parametric form of the given point. Then we find out the points where the tangent and normal intersects the axis. We get a triangle whose centroid’s locus becomes a parabola. We find out the equation of the locus. After getting the equation of that locus we try to find out the vertex, focus, latus-rectum, directrix of that parabolic equation.

Complete step-by-step answer:
Let’s consider a point P on the parabola ${{y}^{2}}=4ax$ in its parametric form. So, $P\equiv \left( a{{t}^{2}},2at \right)$.
For the parabola the equation of tangent and normal at the point $P\left( a{{t}^{2}},2at \right)$ is
$ty=x+a{{t}^{2}}$ and $y=-tx+2at+a{{t}^{3}}$ respectively.
We place all the equations in graphs to get an image form.

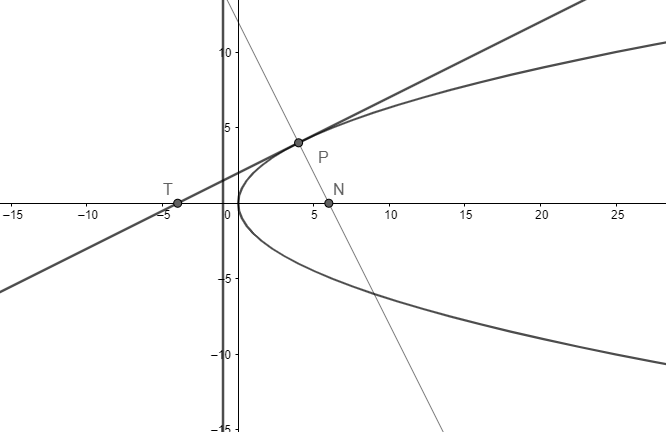
Now the tangent PT meets the axis at point T. As it meets its axis, we can put $y=0$ in the tangent equation to get the point T.
So, $t\times 0=x+a{{t}^{2}}\Rightarrow x=-a{{t}^{2}}$.
The point becomes $T\left( -a{{t}^{2}},0 \right)$.
Similarly, the normal PN meets the axis at point N. As it meets its axis, we can put $y=0$ in the normal equation to get the point N.
So, $0=-tx+2at+a{{t}^{3}}\Rightarrow tx=2at+a{{t}^{3}}\Rightarrow x=a\left( {{t}^{2}}+2 \right)$.
The point becomes $N\left( a\left( {{t}^{2}}+2 \right),0 \right)$. Let centroid of $\Delta PTN$ is $G\left( h,k \right)$.
We know that for three points $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\left( {{x}_{3}},{{y}_{3}} \right)$ of a triangle the centroid will be
$\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$.
So, in case of $\Delta PTN$ the vertices are $P\left( a{{t}^{2}},2at \right),T\left( -a{{t}^{2}},0 \right),N\left( a\left( {{t}^{2}}+2 \right),0 \right)$.
The centroid is $G\equiv \left( \dfrac{a{{t}^{2}}-a{{t}^{2}}+a\left( {{t}^{2}}+2 \right)}{3},\dfrac{2at+0+0}{3} \right)\equiv \left( \dfrac{a\left( {{t}^{2}}+2 \right)}{3},\dfrac{2at}{3} \right)$.
Equating the point, we get $h=\dfrac{a\left( {{t}^{2}}+2 \right)}{3}$ and $k=\dfrac{2at}{3}$.
So, from $k=\dfrac{2at}{3}$ we get that $t=\dfrac{3k}{2a}$.
Putting the value of t in the equation of h we get,
$h=\dfrac{a\left( {{t}^{2}}+2 \right)}{3}=\dfrac{2a+a{{\left( \dfrac{3k}{2a} \right)}^{2}}}{3}$.
From this we get the equation $12ah=8{{a}^{2}}+9{{k}^{2}}$.
This locus of centroid is an equation of parabola. Changing from $\left( h,k \right)$ to $\left( x,y \right)$ we get $\begin{aligned} & 12ax=8{{a}^{2}}+9{{y}^{2}} \\\ & \Rightarrow {{y}^{2}}=\dfrac{4a}{3}\left( x-\dfrac{2a}{3} \right) \\\ \end{aligned}$
The vertex of the parabola is $\left( \dfrac{2a}{3},0 \right)$.
The equation of directrix is $x-\dfrac{2a}{3}=-\dfrac{a}{3}\Rightarrow x=\dfrac{a}{3}$.
Latus rectum is 4 times of the directrix. So, latus rectum length is $\dfrac{4a}{3}$.
The focus will be $\left( \dfrac{2a}{3}+\dfrac{a}{3},0 \right)=\left( a,0 \right)$.

So, the correct answer is “Option A and D”.

Note: We can’t use any normal point by taking normal form. We have to use the parametric form to make it easier to solve the problem. We need to visualize the scenario where the tangent and the normal intersects its axis. As for the normal equation of the parabola ${{y}^{2}}=4ax$ the axis is generally $x=-a$. So, to find the intersecting point we need to use $y=0$. Although we change the final parabolic equation from $\left( h,k \right)$ to $\left( x,y \right)$, it’s not an absolute necessity. We just need to get to the point where we get the equation independent of whatever its variables are.