Question

The tangent at an extremity (in the first quadrant) of latus rectum of the hyperbola $\dfrac{{{x^2}}}{4} - \dfrac{{{y^2}}}{5} = 1$, meets x - axis and y - axis at A and B respectively. Then ${\left( {OA} \right)^2} - {\left( {OB} \right)^2}$, where O is origin equals:
A) $\dfrac{{ - 20}}{9}$
B) $\dfrac{{16}}{9}$
C) $4$
D) $\dfrac{4}{3}$

Answer 1

Here first we will find the values of a and b by comparing the given equation of hyperbola with its standard equation i.e. $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$ and then we will find the value of eccentricity which is given by:-
${b^2} = {a^2}\left( {{e^2} - 1} \right)$ now since the extremity of latus rectum is $\left( {ae,\dfrac{{{b^2}}}{a}} \right)$ hence we will find the latus rectum and then we will find the equation of tangent passing through the latus rectum and then we will find the points A and B by putting x = 0 and y = 0 in the equation of tangent and then find their distance from origin and the compute the required value.

Complete step-by-step answer:

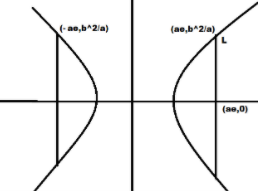
The standard equation of hyperbola is given by:-
$\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$
Comparing the given equation of hyperbola with standard equation we get:-
${a^2} = 4$ $\&$ ${b^2} = 5$……………………..(1)
$\Rightarrow a = 2$ $\&$ $b = \sqrt 5$……………………….(2)
Now eccentricity for standard hyperbola is given by:-
${b^2} = {a^2}\left( {{e^2} - 1} \right)$
Therefore, the eccentricity of the given hyperbola is:-
Putting values from equation 1 we get:-
$5 = 4\left( {{e^2} - 1} \right)$
Calculating the value of e we get:-

$${e^2} = \dfrac{5}{4} + 1 \\\ \Rightarrow {e^2} = \dfrac{{5 + 4}}{4} \\\ \Rightarrow {e^2} = \dfrac{9}{4} \\\$$

Taking square root of both sides we get:-

$$\sqrt {{e^2}} = \sqrt {\dfrac{9}{4}} \\\ e = \dfrac{3}{2} \\\$$

Now since the latus rectum in 1st quadrant is given by:-
$\left( {ae,\dfrac{{{b^2}}}{a}} \right)$
Hence putting in the respective values from equation 1 and 2 we get:-
${\text{latus rectum}} \equiv \left( {2 \times \dfrac{3}{2},\dfrac{5}{2}} \right)$
Simplifying it we get:-
${\text{latus rectum}} \equiv \left( {3,\dfrac{5}{2}} \right)$
Now we will find the equation of tangent of the given hyperbola.
The standard equation of tangent of hyperbola passing through $\left( {{x_1},{y_1}} \right)$ is given by:-
$\dfrac{{x{x_1}}}{{{a^2}}} - \dfrac{{y{y_1}}}{{{b^2}}} = 1$
Now since it is given that the tangent passes through the latus rectum hence its equation is given by:-
$\dfrac{{x\left( 3 \right)}}{4} - \dfrac{{y\left( {\dfrac{5}{2}} \right)}}{5} = 1$
Simplifying it further we get:-

$$\dfrac{{x\left( 3 \right)}}{4} - \dfrac{{5y}}{{2 \times 5}} = 1 \\\ \Rightarrow \dfrac{{3x}}{4} - \dfrac{y}{2} = 1 \\\$$

Now it is given that the tangent meets x axis at A hence y=0
Putting y=0 in above equation we get:-
$\dfrac{{3x}}{4} - \dfrac{0}{2} = 1$
Solving for x we get:-

$$\dfrac{{3x}}{4} = 1 \\\ x = \dfrac{4}{3} \\\$$

Hence point A is $A \equiv \left( {\dfrac{4}{3},0} \right)$
Now it is given that the tangent meets y axis at B hence x=0
Putting x=0 in above equation we get:-
$\dfrac{{3\left( 0 \right)}}{4} - \dfrac{y}{2} = 1$
Solving for y we get:-

$$\dfrac{{ - y}}{2} = 1 \\\ y = - 2 \\\$$

Hence point B is $B \equiv \left( {0, - 2} \right)$
Now we will find the distance of Point A from origin (0, 0).
The distance between two points $\left( {{x_1},{y_1}} \right)\& \left( {{x_2},{y_2}} \right)$ is given by:-
$d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
Putting the values for point A and origin we get:-
$OA = \sqrt {{{\left( {\dfrac{4}{3} - 0} \right)}^2} + {{\left( {0 - 0} \right)}^2}}$
Simplifying it further we get:-

$$OA = \sqrt {{{\left( {\dfrac{4}{3}} \right)}^2}} \\\ \Rightarrow OA = \dfrac{4}{3} \\\$$

Now we will find the distance of Point B from origin (0, 0).
The distance between two points $\left( {{x_1},{y_1}} \right)\& \left( {{x_2},{y_2}} \right)$ is given by:-
$d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
Putting the values for point A and origin we get:-
$OB = \sqrt {{{\left( {0 - 0} \right)}^2} + {{\left( { - 2 - 0} \right)}^2}}$
Simplifying it further we get:-

$$OB = \sqrt {{{\left( { - 2} \right)}^2}} \\\ \Rightarrow OB = \sqrt 4 \\\ \Rightarrow OB = 2 \\\$$

Now we will evaluate the value of ${\left( {OA} \right)^2} - {\left( {OB} \right)^2}$
Putting in the respective values we get:-
${\left( {OA} \right)^2} - {\left( {OB} \right)^2} = {\left( {\dfrac{4}{3}} \right)^2} - {\left( 2 \right)^2}$
Simplifying it further we get:-
${\left( {OA} \right)^2} - {\left( {OB} \right)^2} = \dfrac{{16}}{9} - 4$
Taking the LCM we get:-
${\left( {OA} \right)^2} - {\left( {OB} \right)^2} = \dfrac{{16 - 4\left( 9 \right)}}{9}$
Solving it further we get:-

$$\Rightarrow {\left( {OA} \right)^2} - {\left( {OB} \right)^2} = \dfrac{{16 - 36}}{9} \\\ \Rightarrow {\left( {OA} \right)^2} - {\left( {OB} \right)^2} = \dfrac{{ - 20}}{9} \\\$$

So, the correct answer is “Option A”.

Note: Students should take a note that the coordinate of latus rectum in first quadrant is given by:-
$\left( {ae,\dfrac{{{b^2}}}{a}} \right)$
Also, all the points and calculations should be evaluated carefully to get the correct answer.