Question

The tangent and normal to the ellipse $3{{x}^{2}}+5{{y}^{2}}=32$ ate the point P ( 2, 2 ) meet the x – axis at Q and R respectively. Then the area of triangle PQR is :
(a) $\dfrac{14}{3}$
(b)$\dfrac{16}{3}$
(c)$\dfrac{68}{15}$
(d)$\dfrac{34}{15}$

Answer 1

First we will find equation of ellipse in standard form which is $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$, then we will find the equation of normal which is $\dfrac{x{{x}_{1}}}{{{a}^{2}}}+\dfrac{y{{y}_{1}}}{{{b}^{2}}}=1$ and tangent which cuts point P ( 2, 2) and x – axis and then using area of triangle we will evaluate the area of triangle by formula $\dfrac{1}{2}\times b\times h$ , where b denotes base and h denotes height of triangle.

Complete step-by-step answer:
We have the equation of ellipse in question equals $3{{x}^{2}}+5{{y}^{2}}=32$. We know that general equation of ellipse is $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ .
So, writing the equation of ellipse $3{{x}^{2}}+5{{y}^{2}}=32$ in standard form $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$, we get
$\dfrac{{{x}^{2}}}{\left( \dfrac{32}{3} \right)}+\dfrac{{{y}^{2}}}{\left( \dfrac{32}{5} \right)}=1$
On comparing, we get ${{a}^{2}}=\dfrac{32}{3}$ and ${{b}^{2}}=\dfrac{32}{5}$.

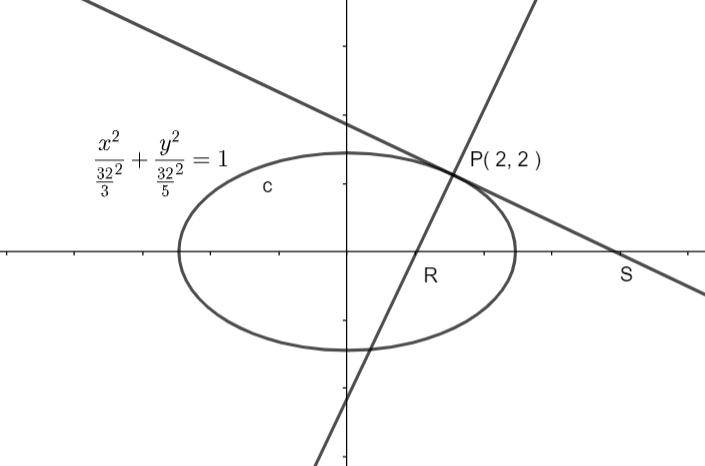
Now, let PS be the tangent of ellipse at point P ( 2, 2 ).
We know that equation of tangent of ellipse is $\dfrac{x{{x}_{1}}}{{{a}^{2}}}+\dfrac{y{{y}_{1}}}{{{b}^{2}}}=1$
So , at ( 2, 2 ) we get
$\dfrac{2x}{{{a}^{2}}}+\dfrac{2y}{{{b}^{2}}}=1$
And we have ${{a}^{2}}=\dfrac{32}{3}$ and ${{b}^{2}}=\dfrac{32}{5}$.
So, $\dfrac{3\cdot 2x}{32}+\dfrac{5\cdot 2y}{32}=1$
On solving we get
3 x + 5 y = 16, which is an equation tangent on the ellipse at point P ( 2, 2 ).
Now, slope of tangent 3 x + 5 y = 16 can be easily find by comparing it with y = mx + c,
So, re – writing 3 x + 5 y = 16 as,
$y=-\dfrac{3}{5}x+16$
So, slope of tangent will be ${{m}_{T}}=-\dfrac{3}{5}$
As S lies on the x – axis and equation of tangent, so y value will be zero.
So coordinate of S, will be
3 x + 5 ( 0 ) = 16
$x=\dfrac{16}{3}$
So, we have $S\left( \dfrac{16}{3},0 \right)$
Now, we know that the slope of normal is negative or reciprocal of slope of tangent.
So, slope of normal is ${{m}_{N}}=\dfrac{5}{3}$
As normal passes from ( 2, 2 ) so, equation of normal will be
$(y-2)=\dfrac{5}{3}(x-2)$
On solving we get
3 y – 6 = 5x – 10
Or, 3y – 5x + 4 = 0
Now, as point R lies on x – axis and equation of normal, so value of y will be zero,
So, 3 ( 0 ) – 5x + 4 = 0
Or, $x=\dfrac{4}{5}$
So, $R\left( \dfrac{4}{5},0 \right)$
Now, Area of PRS can be found by formula of triangle $\dfrac{1}{2}\times b\times h$ , where b denotes base and h denotes height of triangle.
Now, from figure we can easily see that height is 2 as P is ( 2, 2 ) and base b will be $b=\dfrac{16}{3}-\dfrac{4}{5}$
On, solving we get $b=\dfrac{68}{15}$
So, area of triangle PRS $=\dfrac{1}{2}\times \dfrac{68}{15}\times 2$
On solving we will get,
$=\dfrac{68}{15}$

So, the correct answer is “Option c”.

Note: Always remember some general formula such as standard form of ellipse is $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$, slope form of line is y = mx + c, equation of tangent on ellipse at any point ( p, r ) is $\dfrac{xp}{{{a}^{2}}}+\dfrac{yr}{{{b}^{2}}}=1$ and also that of normal is negative of reciprocal of slope of tangent. Avoid calculation mistakes.